Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Định lí: "Hai góc cùng phụ một góc thứ ba thì bằng nhau".
Hình vẽ:
O123
Giả thiết - Kết luận:
| GT |
\widehat{O_1} + \widehat{O_2} = 90^{\circ}O1+O2=90∘ \widehat{O_2} + \widehat{O_3} = 90^{\circ}O2+O3=90∘ |
| KL | \widehat{O_1} = \widehat{O_3}O1=O3 |
Định lí: "Hai góc cùng phụ một góc thứ ba thì bằng nhau".
Hình vẽ:
O123
Giả thiết - Kết luận:
| GT |
\widehat{O_1} + \widehat{O_2} = 90^{\circ}O1+O2=90∘ \widehat{O_2} + \widehat{O_3} = 90^{\circ}O2+O3=90∘ |
| KL | \widehat{O_1} = \widehat{O_3}O1=O3 |

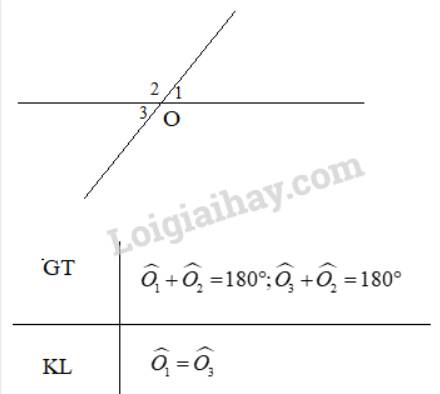
Giả sử \(\widehat {{O_1}},\widehat {{O_3}}\) cùng bù với góc \(\widehat {{O_2}}\). Ta được:
\(\widehat {{O_1}} + \widehat {{O_2}} = 180^\circ ;\widehat {{O_3}} + \widehat {{O_2}} = 180^\circ \)
\( \Rightarrow \widehat {{O_1}} =180^\circ -\widehat {{O_2}}; \widehat {{O_3}}=180^\circ -\widehat {{O_2}}\)
\( \Rightarrow \widehat {{O_1}} = \widehat {{O_3}}\) (đpcm)

Bài 1:
| GT | \(\widehat{A}+\widehat{B}=90^0;\widehat{C}+\widehat{B}=90^0\) |
| KL | \(\widehat{A}=\widehat{C}\) |
Ta có: \(\widehat{A}+\widehat{B}=90^0\)
nên \(\widehat{A}=90^0-\widehat{B}\left(1\right)\)
Ta có: \(\widehat{C}+\widehat{B}=90^0\)
nên \(\widehat{C}=90^0-\widehat{B}\left(2\right)\)
Từ (1) và (2) suy ra \(\widehat{A}=\widehat{C}\)

ĐL 1: GT: góc A + Góc C = ; góc B + Góc C =
KL:Góc A = góc B
CM: góc A+C=góc B+C=
A+C-C=B+C-C (bỏ chữ góc cho gọn nhé)
A=B(dpcm)
ĐL2: góc A + Góc C = ; góc B + Góc C =
KL:Góc A = góc B
CM: A+C=góc B+C=
A+C-C=B+C-C
A=B(dpcm)
a. gt:hai góc cùng phụ
kl:hai góc bằng nhau
giai : goi hai góc a va b cùng phụ với c ta dược
a+c=90 =>a=90-c
b+c=90=>b=90-c
từ 2 điều trên suy ra a=b
b. tương tụ trên chỉ cwnf thay phụ thành bù. 90 thanh 180


Giả sử \(\widehat A,\widehat C\) cùng phụ với \(\widehat B\). Ta được:
\(\widehat A + \widehat B = 90^\circ ;\widehat C + \widehat B = 90^\circ \)
\(\widehat A = 90^\circ - \widehat B;\widehat C = 90^\circ - \widehat B\)
\( \Rightarrow \widehat A = \widehat C\) (đpcm)