Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

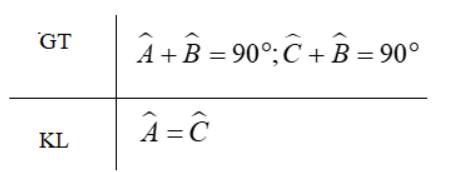
Giả sử \(\widehat A,\widehat C\) cùng phụ với \(\widehat B\). Ta được:
\(\widehat A + \widehat B = 90^\circ ;\widehat C + \widehat B = 90^\circ \)
\(\widehat A = 90^\circ - \widehat B;\widehat C = 90^\circ - \widehat B\)
\( \Rightarrow \widehat A = \widehat C\) (đpcm)

Bài 1:
| GT | \(\widehat{A}+\widehat{B}=90^0;\widehat{C}+\widehat{B}=90^0\) |
| KL | \(\widehat{A}=\widehat{C}\) |
Ta có: \(\widehat{A}+\widehat{B}=90^0\)
nên \(\widehat{A}=90^0-\widehat{B}\left(1\right)\)
Ta có: \(\widehat{C}+\widehat{B}=90^0\)
nên \(\widehat{C}=90^0-\widehat{B}\left(2\right)\)
Từ (1) và (2) suy ra \(\widehat{A}=\widehat{C}\)

ĐL 1: GT: góc A + Góc C = ; góc B + Góc C =
KL:Góc A = góc B
CM: góc A+C=góc B+C=
A+C-C=B+C-C (bỏ chữ góc cho gọn nhé)
A=B(dpcm)
ĐL2: góc A + Góc C = ; góc B + Góc C =
KL:Góc A = góc B
CM: A+C=góc B+C=
A+C-C=B+C-C
A=B(dpcm)
a. gt:hai góc cùng phụ
kl:hai góc bằng nhau
giai : goi hai góc a va b cùng phụ với c ta dược
a+c=90 =>a=90-c
b+c=90=>b=90-c
từ 2 điều trên suy ra a=b
b. tương tụ trên chỉ cwnf thay phụ thành bù. 90 thanh 180


GT: x bù vs z ; y bù vs z
KL: x = y
CM: ta có x + z = 1800 (1)
y + z = 1800 (2)
từ (1) và (2) => x=y



A. Phương pháp “So sánh hai đoạn thẳng”.
Để chứng minh hai đoạn thẳng bằng nhau ta có thể sử dụng một trong các phương pháp sau đây:
1)
Trong một tam giác cân, hai cạnh bên bằng nhau.
Trong một tam giác đều, các cạnh bằng nhau.
Các cạnh của đa giác đều thì bằng nhau.
2) Trong hai tam giác bằng nhau thì các cạnh tương ứng bằng nhau.
3)
Hai đoạn thẳng cùng bằng một đoạn thẳng thứ ba thì bằng nhau.
Trung tuyến thuộc cạnh huyền của một tam giác vuông thì bằng một nửa cạnh huyền.
Đường trung bình ứng với một cạnh của tam giác thì bằng một nửa cạnh ấy.
Đường trung trực của đoạn thẳng chia đoạn thẳng ấy thành hai đoạn thẳng bằng nhau.
Đường trung tuyến của tam giác chia cạnh tương ứng thành hai đoạn thẳng bằng nhau.
a. Trong một hình bình hành:
– Các cạnh đối diện thì bằng nhau.
– Các đường chéo cắt nhau tại trung điểm của mỗi đường.
b. Trong một hình thang cân:
Hai cạnh bên thì bằng nhau.
Hai đường chéo thì bằng nhau.
c. Trong một hình chữ nhật:
Các cạnh đối diện thì bằng nhau.
Các đường chéo cắt nhau tại trung điểm của mỗi đường.
Hai đường chéo thì bằng nhau.
d. Trong một hình thoi:
Các cạnh bên thì bằng nhau.
Các đường chéo cắt nhau tại trung điểm của mỗi đường.
e. Hình vuông có tất cả các tính chất trên.
f. Trong một đường tròn hay hai đường tròn bằng nhau:
Các dây cách đều tâm thì bằng nhau.
Các dây trương các cung bằng nhau thì bằng nhau.
g. Hai tiếp tuyến phát xuất từ một điểm đến một đường tròn thì bằng nhau.
h. Một điểm nằm trên tia phân giác của một góc thì cách đều hai cạnh của góc ấy.
i. Hai đoạn thẳng cùng nghiệm đúng một hệ thức thì bằng nhau.
Để chứng minh đoạn thẳng a lớn hơn đoạn thẳng b, ta có thể sử dụng một trong các phương pháp sau đây:
1) Hai đoạn thẳng a và b là hai đoạn thẳng dối diện với hai góc A và B của tam giác ABC và . A > B
2) a = m + n và b, m, n là độ dài ba cạnh của tam giác.
3) a là độ dài cạnh huyền và b là độ dài của cạnh góc vuông của tam giác vuông.
4) a và b là hai dây cung của một đường tròn (hay hai đường tròn bằng nhau) mà khoảng cách từ tâm đường tròn đến a nhỏ hơn khoảng cách từ tâm đường tròn đến b.
5) Cung nhỏ của đường tròn trương dây a lớn hơn cung nhỏ của đường tròn trương dây b.
6) Góc nội tiếp của đường tròn chắn dây cung a lớn hơn góc nội tiếp của đường tròn đó chắn dây cung b.
Phương pháp Chứng minh Hình học HọC SINH GIỏI Giáo viên: Đinh Vũ Hưng Trang 2
7) Nếu a = b thì sẽ đưa đến một điều vô lý.
áp dụng: Các Bài tập dành cho “ tất cả học sinh”
1) Cho hình thang ABCD. Đường phân giác của góc A cắt cạnh BC tại một điểm E. Cm: AB = BE.
2) Cho tam giác ABC. Trong nửa mặt phẳng bờ AB có chứa điểm C, ta dựng đường vuông góc với AB tại A và lấy trên đó một điểm D sao cho AD = AB. Trên nửa mặt phẳng bờ AC có chứa điểm B ta dựng đường vuông góc với AB tại A và lấy trên đó một điểm E sao cho AE = AC. Chứng minh CD = BE.
3) Trên tia phân giác của một góc nhọn xOy ta lấy một điểm A. Vẽ hai đường tròn bất kỳ đi qua O và A. Đường tròn thứ nhất cắt Ox ở M và cắt Oy ở P. Đường tròn thứ hai cắt Ox ở N và Oy ở Q. Chứng minh MN = PQ.
4) Cho tam giác ABC có ba góc nhọn. Kẻ hai đường cao BI và CK. Gọi M là trung điểm của cạnh BC. Chứng minh MI = MK.
5) Cho tam giác ABC và trung tuyến AM thuộc cạnh BC. Trên tia đối của tia MA lấy điểm D sao cho MD = MA. Chứng minh BD = AC.
6) Cho đường tròn dường kính AB. Từ A và B kẻ hai dây cung bất kỳ song song với nhau, hai dây cung này cắt đường tròn lần lượt tại C
Giả sử \(\widehat {{O_1}},\widehat {{O_3}}\) cùng bù với góc \(\widehat {{O_2}}\). Ta được:
\(\widehat {{O_1}} + \widehat {{O_2}} = 180^\circ ;\widehat {{O_3}} + \widehat {{O_2}} = 180^\circ \)
\( \Rightarrow \widehat {{O_1}} =180^\circ -\widehat {{O_2}}; \widehat {{O_3}}=180^\circ -\widehat {{O_2}}\)
\( \Rightarrow \widehat {{O_1}} = \widehat {{O_3}}\) (đpcm)