Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(=\dfrac{135.1420+4,5.3.10.78}{\left(3+27\right).9:2}\)
\(=\dfrac{135.1420+135.78}{30.9:2}\)
\(=\dfrac{135.\left(1420+78\right)}{135}\)
\(=1498\)
A = \(\dfrac{135\times1420+4,5\times780\times3}{3+6+9+...+24+27}\)
Đặt Tử số là B; Mẫu số là C trong đó B và C lần lượt là:
B = 135 \(\times\) 1420 + 4,5 \(\times\) 780 \(\times\) 3
C = 3 + 6 + 9 +....+24 + 27
A = \(\dfrac{B}{C}\)
B = 135 \(\times\) 1420 + 4,5 \(\times\) 780 \(\times\) 3
B = 135 \(\times\) 1420 + 45 \(\times\) 78 \(\times\) 3
B = 135 \(\times\) 1420 + (45 \(\times\) 3) \(\times\) 78
B = 135 \(\times\) 1420 + 135 \(\times\) 78
B = 135 \(\times\) ( 1420 + 78)
B = 135 \(\times\) 1498
C = 3 + 6 + 9+...+ 24+27
Dãy số trên là dãy số cách đều vơi khoảng cách là: 6 - 3 = 3
Số số hạng của dãy số trên là: (27 - 3): 3 + 1 = 9
Tổng C là: C = (27 + 3)\(\times\) 9 : 2 = 135
A = \(\dfrac{B}{C}\) = \(\dfrac{135\times1498}{135}\) = 1498
A = \(\dfrac{13,5x1420+4,5x780x3}{3+6+9+...+24+27}\)
Tính giá trị biểu thức , giúp mik với cảm ơn :D

\(A=\dfrac{13,5\cdot1420+4,5\cdot780\cdot3}{3+6+9+...+24+27}\)
Gọi tử số là a, mẫu số là b
ta có a=13,5*1420+4,5*780*3=13,5*1420+13,5*780=13,5*(1420+780)=13,5*2200=29700
ta có b: số số hạng của b: (27-3)/3+1=9(số hạng)
tổng của b: (27+3)*9/2=135
=> \(\dfrac{29700}{135}=220\). vậy A=220

A=99-97+...+7-5+3-1
=[99-97]+..+[7-5]+[3-1]
=2+...+2+2
=2*50
100
A=99 - 97 + 95 - 93 + 91 - 89 + ... + 7 - 5 + 3 - 1
Ta thấy khoảng cách giữa 2 số liên tiếp là 2
-> Số lượng số hạng của dãy là :(99-1)/2 + 1 =50
Mà cứ 2 số là 1 cặp => có 50/2 =25 cặp tất cả
Vậy A=99 - 97 + 95 - 93 + 91 - 89 + ... + 7 - 5 + 3 - 1
= (99-97)+(95-93)+(91-89)+.....+(7-5)+(3-1)
= 2*25
=50

a) \(M=\frac{2\times2}{1\times5}+\frac{2\times2}{5\times9}+\frac{2\times2}{9\times13}+...+\frac{2\times2}{45\times40}\)
\(M=\frac{4}{1\times5}+\frac{4}{5\times9}+\frac{4}{9\times13}+...+\frac{4}{45\times49}\)
\(M=1-\frac{1}{5}+\frac{1}{5}-\frac{1}{9}+\frac{1}{9}-\frac{1}{13}+...+\frac{1}{45}-\frac{1}{49}\)
\(M=1-\frac{1}{49}\)
\(M=\frac{48}{49}\)
b) \(\frac{1}{1+2}+\frac{1}{1+2+3}+\frac{1}{1+2+3+4}+...+\frac{1}{1+2+3+4+5+...+10}\)
= \(\frac{2}{2\times\left(1+2\right)}+\frac{2}{2\times\left(1+2+3\right)}+...+\frac{2}{2\times\left(1+2+3+...+10\right)}\)
\(=\frac{2}{6}+\frac{2}{12}+...+\frac{2}{110}\)
\(=\frac{2}{2\times3}+\frac{2}{3\times4}+...+\frac{2}{10\times11}\)
\(=2\times\left(\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{10}-\frac{1}{11}\right)\)
\(=2\times\left(\frac{1}{2}-\frac{1}{11}\right)\)
\(=2\times\frac{9}{22}\)
\(=\frac{9}{11}\)
Mình trả lời câu a nha M= 4/1*5+4/5*9+4/9*13+...+4/45*49 M=1-1/5+1/5-1/9+1/9-1/13+...+1/45-1/49 M=1-1/49=48/49
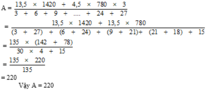
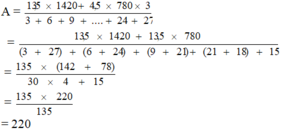
\(A=\dfrac{135x1420+4,5x780x3}{3+6+9...+24+27}\\ =\dfrac{135x1420+4,5x3x10x78}{\left(3+27\right)x9:2}\\ =\dfrac{135x1420+135x78}{30x9:2}\\ =\dfrac{135x\left(1420+78\right)}{135}\\ =1420+78=1498\)