K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HY
21 tháng 4 2017
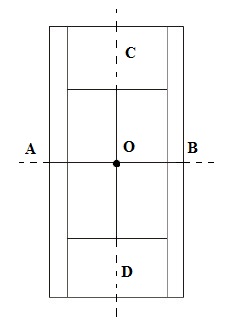
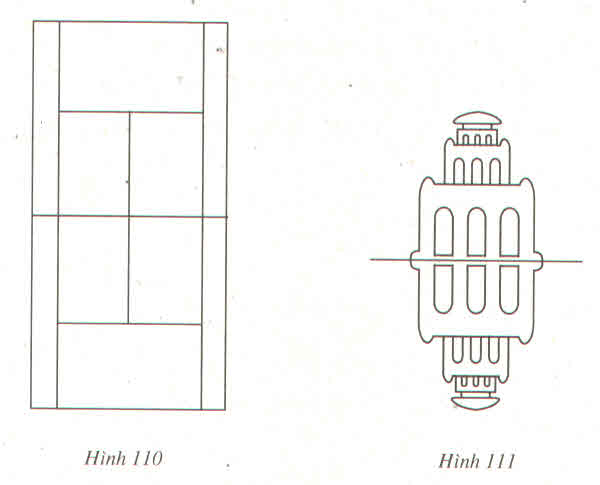
a) Hình 110 (sân quần vợt) có hai trục đối xứng, có một tâm đối xứng.
-Hai trục đối xứng AB và CD.
-Một tâm đối xứng là O.
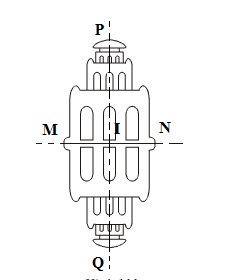
b) Hình 111 (Tháp Rùa và bóng của nó trên mặt nước) có hai trục đối xứng, có một tâm đối xứng.
-Hai trục đối xứng là MN và PQ.
- Một tâm đối xứng là I.
AT
21 tháng 4 2017
a) Hình 45 (sân quần vợt) có hai trục đối xứng, có một tâm đối xứng.
- Hai trục đối xứng AB và CD.
- Một tâm đối xứng là O.
b) Hình 46 (Tháp Rùa và bóng của nó trên mặt nước) có hai trục đối xứng, có một tâm đối xứng.
- Hai trục đối xứng là MN và PQ
- Một tâm đối xứng là I.
6 tháng 1 2021
Những hình có trục đối xứng là: đường tròn, tam giác cân, tam giác đều, hình thang cân, hình thoi, hình vuông, hình chữ nhật
Những hình có tâm đối xứng là: đường tròn, hình bình hành, hình chữ nhật, hình thoi, hình vuông
Những hình vừa có tâm đối xứng vừa có trục đối xứng là: hình chữ nhật, hình thoi, hình vuông
29 tháng 11 2018
Tứ giác: 0 trục, 0 tâm
Hình thang 0 trục, 0 tâm
Hình thang cân 1 trục 0 tâm
Hình bình hành 0 trục 1 tâm
Hình chữ nhật 2 trục 1 tâm
Hình thoi 2 trục 1 tâm
Hình vuông 4 trục 1 tâm
5 tháng 10 2022
Tứ giác: 0 trục đối xứng, 0 tâm đối xứng
Hình thang: 0 trục đối xứng, 0 tâm đối xứng
Hình thang cân: 1 trục đối xứng, 0 tâm đối xứng
Hình bình hành: 0 trục đối xứng, 1 tâm đối xứng
Hình chữ nhật: 2 trục đối xứng, 1 tâm đối xứng
Hình thoi: 2 trục đối xứng, 1 tâm đối xứng
Hình vuông: 4 trục đối xứng, 1 tâm đối xứng
Tích đúng 5 sao cho mình nhé.
OK bạn
TL
1
CH
Cô Hoàng Huyền
Admin
VIP
1 tháng 11 2016
Tính chất đối xứng - Toán lớp 8 [Online Math - olm.vn] - YouTube
Em có thể xem bài giảng tại đây nhé, ở đó cô đã trình bày rõ hai loại đối xứng tâm và đối xứng trục.
B
21 tháng 4 2017
Chú ý:
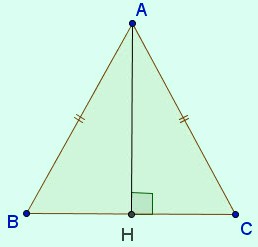
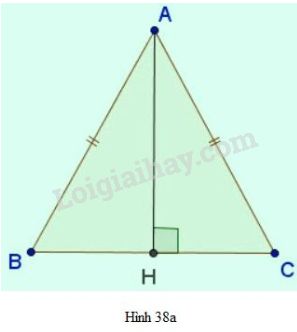
- ∆ABC cân tại A có trục đối xứng là đường phân giác của góc BAC.
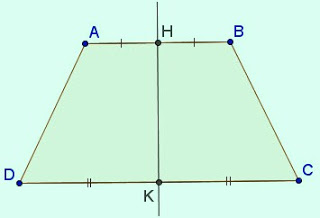
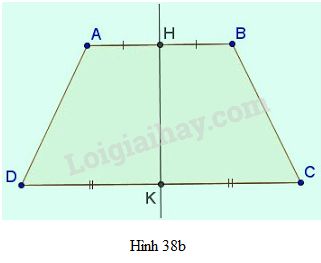
- Hình thang cân nhận đường thẳng đi qua trung điểm hai đáy làm trục đối xứng.
Đối với tam giác cân hình 38a:
# Đối với hình thang cân hình 38b:Tam giác cân ABC, trục đối xứng là đường cao AH với H là trung điểm của đoạn BC.
Hình thang cân ABCD (AB // CD), trục đối xứng là đường thẳng KH với K, H lần lượt là trung điểm của AB và CD.
TT
6
NA
7 tháng 10 2018
Hình nào vừa có trục đối xứng, vừa có tâm đối xứng ?
- Hình vuông
- Hình tròn
....
7 tháng 10 2018
Hình nào vừa có trục đối xứng, vừa có tâm đối xứng ?
Trả lời:
Hình binhhf hành
hình vuông
hình chữ nhật
18 tháng 11 2019
Tự vẽ hình
a) Ta có: AB = CD (cạnh hình thoi)
BE = DG (g.t)
=> AB + BE = CD + DG hay AE = CG (cmt)
Xét tam giác AHE và tam giác CFG ta có:
AE=CG
HAE = FCG (cùng bù vs BAD = DCB)
AH=CF (gt)
Do đó tam giác AHE = tam giác CFG (c.g.c) => HE = FG
Do đó EFGH là cạnh bình hành (đpcm)
b) Nối E vs G
Xét tam giác OBE và tam giác ODG ta có:
BE= DG (gt)
OBE = ODG (so le trong)
OB = OD ( tính chất đường chéo của hình thoi ABCD)
=> tam giác OBE = tam giác ODG (c.g.c) => OBE = ODG
Mà DOG + GOB = 180o ⇒ ba điểm G, O, E thẳng hàng.
Chứng minh tương tự ta có H, O, F thẳng hàng.
Vậy O là tâm đối xứng của hình bình hành EFGH.
c) Hình bình hành EFGH là hình thoi ⇔ HE = EF
\(\Leftrightarrow\Delta HAE=\Delta EBF\left(c.c.c\right)\)
\(\Leftrightarrow\widehat{HAE}=\widehat{EBF}=\widehat{EDA}\left(đv\right)\)
\(\Leftrightarrow\widehat{HAE}=\widehat{EAD}\) mà \(\widehat{HAE}+\widehat{EAD=180^O\left(kb\right)}\)
\(\Leftrightarrow\widehat{HAE}=\widehat{EAD}=90^O\)
⇔ Hình thoi ABCD có 1 góc vuông
⇔ ABCD là hình vuông.
Vậy hình thoi ABCD phải là hình vuông thì hình bình hành EFGH trở thành hình thoi.
16 tháng 12 2020
a) Ta có AB = CD (cạnh hình thoi)
BE = DG (gt)
⇒ AB + BE = CD + DG hay AE = CG (cmt)
Xét ΔAHE và ΔCFG có:
AE = CG
∠HAE = ∠FCG (cùng bù với ∠BAD = ∠DCB ),
AH = CF (gt)
Do đó ΔAHE = ΔCFG (c.g.c) ⇒ HE = FG
Chứng minh tương tự ta có HG = EF
Do đó tứ giác EFGH là hình bình hành (các cạnh đối bằng nhau).
b) Nối E và G.
Xét ΔOBE và ΔODG có
BE = DG (gt),
∠OBE = ∠ODG (so le trong),
OB = OD ( tính chất đường chéo của hình thoi ABCD)
⇒ ΔOBE = ΔODG (c.g.c) ⇒ ∠OBE = ∠ODG
Mà ∠DOG + ∠GOB = 180o ⇒ ba điểm G, O, E thẳng hàng.
Chứng minh tương tự ta có H, O, F thẳng hàng.
Vậy O là tâm đối xứng của hình bình hành EFGH.
c) Hình bình hành EFGH là hình thoi ⇔ HE = EF
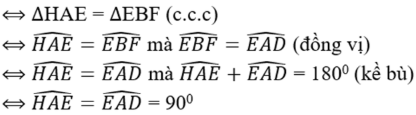
⇔ Hình thoi ABCD có 1 góc vuông
⇔ ABCD là hình vuông.
Vậy hình thoi ABCD phải là hình vuông thì hình bình hành EFGH trở thành hình thoi.
VUÔNG
Hình vuông