Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Phương trình mặt phẳng trung trực của AB là 
Đường thẳng cần tìm d cách đều hai điểm A, B nên sẽ thuộc mặt phẳng α
Lại có 
hay 
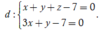
Chọn x = t ta được: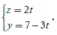 
Chọn C.
Chọn A
Gọi (Q) là mặt phẳng trung trực của đoạn thẳng AB
=> Mọi điểm thuộc (Q) đều cách đều AB
Để mọi điểm nằm trên d đều cách đều AB thì d phải thuộc Q
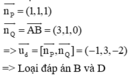
Đường thẳng d nằm trong cả (P) và (Q) => d phải đi qua 1 điểm nằm trong cả (P) và (Q)
Gọi điểm chung này là E
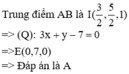
Kiểm tra ta thấy d cắt (P)
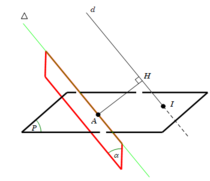
Đường thẳng cần tìm là giao tuyến của mặt phẳng α với mặt phẳng (P)
Trong đó mặt phẳng α đi qua điểm A và vuông góc với đường thẳng AH, điểm H là hình chiếu của A trên đường thẳng d
Ta tìm được tọa độ điểm H(-1;0;2) => phương trình mp
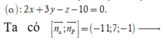đường thẳng
∆
có một VTVP là
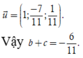
Chọn A.
Đáp án B
Vì 
mà 
Vì M là hình chiếu vuông góc của I trên ∆ 
Khi đó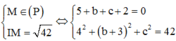 
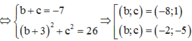
Vậy M(5; - 2; - 5) hoặc M(5; - 8;1) → bc=10
