Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C.
Phương pháp:
- Viết phương trình mặt phẳng α .
- Tìm tọa độ giao điểm B, C của α với trục Oy, Oz.
- Tính thể tích khối tứ diện vuông OABC: V = 1 6 . O A . O B . O C .
Cách giải:
Giả sử n → a ; b ; c , a 2 + b 2 + c 2 ≠ 0 là một vecto pháp tuyến của (P).
Vì α đi qua A 2 ; 0 ; 0 nên PTTQ của (P):
a x − 2 + b y − 0 + c z − 0 = 0
⇔ a x + b y + c z − 2 a = 0.
Vì α vuông góc với α nên n → a ; b ; c vuông góc với n 1 → 0 ; 2 ; − 1 .
Khi đó,
0. a + 2. b + − 1 . c = 0 ⇔ c = 2 b
⇒ α : a x + b y + 2 b z − 2 a = 0
d O ; α = 4 3 ⇔ − 2 a a 2 + b 2 + 4 b 2 = 4 3 ⇔ 6 a 2 = 16 a 2 + 5 b 2 ⇔ a 2 = 4 b 2 ⇔ a = 2 b a = − 2 b
Cho
b = 1 ⇒ a = 2 a = − 2 ⇒ n → 2 ; 1 ; 2 n → − 2 ; 1 ; 2 ⇒ α : 2 x + y + 2 z − 4 = 0 α : − 2 x + y + 2 z + 4 = 0
+ ) α : 2 x + y + 2 z − 4 = 0 ⇒ B 0 ; 4 ; 0 , C 0 ; 0 ; 2 ⇒ V O A B C = 1 6 . 2 . 4 . 2 = 8 3
+ ) α : − 2 x + y + 2 z + 4 = 0 ⇒ B 0 ; − 4 ; 0 , C 0 ; 0 ; − 2 ⇒ V O A B C = 1 6 . 2 . − 4 . − 2 = 8 3
Vậy thể tích khối tứ diện OABC là 8 3 .

HD: Gọi tọa độ ba điểm A, B, C lần lượt là

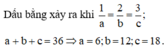
Vậy độ dài ba cạnh OA, OB, OC lần lượt theo thứ tự lập thành cấp số cộng. Chọn C.

vì (C) đi qua điểm A nên tọa độ điểm A thỏa mãn pt \(y=\frac{ax^2-bx}{x-1}\) ta có \(\frac{5}{2}=\frac{a+b}{-2}\Rightarrow a+b=-5\)
vì tiếp tuyến của đồ thị tại điểm O có hệ số góc =-3 suy ra y'(O)=-3
ta có \(y'=\frac{ax^2-2ax+b}{\left(x-1\right)^2}\) ta có y'(O)=b=-3 suy ra a=-2
vậy ta tìm đc a và b
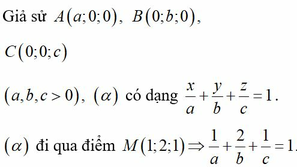
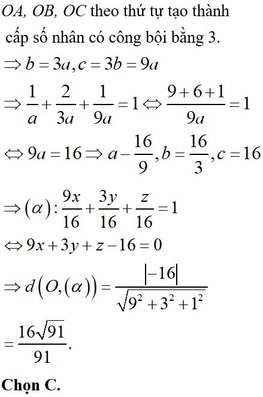

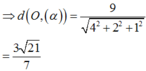
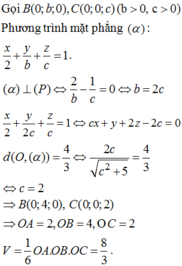



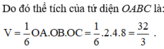

Đáp án C