Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng công thức
F = G M n R 2 = 6 , 67.10 − 11 2.10 30 .6.10 24 1 , 5.10 11 2 = 3 , 557.10 22 N

\(F_{hapdan}=G\dfrac{m'm''}{r^2}=6,67\cdot10^{-11}\dfrac{6\cdot10^{24}\cdot7,2\cdot10^{22}}{\left(3,8\cdot10^5\cdot1000\right)^2}=.......\left(N\right)\)
\(F=G\cdot\dfrac{M_1M_2}{d^2}=6,67\cdot10^{-11}\cdot\dfrac{6\cdot10^{24}\cdot7,2\cdot10^{22}}{\left(3,8\cdot10^5\cdot10^3\right)^2}=2\cdot10^{20}\)(N)
Chọn C

Chu kì chuyển động của Mặt Trăng quanh Trái Đất là : T 1 = 365 13 = 28 (ngày)
Chu kì chuyển động của Trái Đất quanh Mặt Trời là: T 2 = 365 ( ngày)
Khi Mặt Trăng chuyển động tròn quanh Trái Đất thì lực hấp dẫn giữa Mặt Trăng và Trái Đất đóng vai trò là lực hướng tâm, nên: F h d = F h t ⇔ G m M r 2 = m v 2 r ⇔ G M r = v 2
Mà: v = ω r = 2 π T r
↔ G M r 1 = 4 π 2 T 1 2 r 1 2 → M = 4 π 2 T 1 2 G r 1 3
Khi Trái Đất chuyển động tròn quanh Mặt Trời thì lực hấp dẫn giữa Trái Đất và Mặt Trời đóng vai trò là lực hướng tâm, nên:
F h d = F h t ⇔ G m M r 2 = m v 2 r ⇔ G M r = v 2
Mà: v = ω r = 2 π T r
↔ G M m t r 2 = 4 π 2 T 2 2 r 2 2 → M m t = 4 π 2 T 2 2 G r 2 3
Tỉ số khối lượng của Mặt Trời và Trái Đất
M m t M = 4 π 2 T 2 2 G r 2 3 4 π 2 T 1 2 G r 1 3 = T 1 2 r 2 3 T 2 2 r 1 3 = ( T 1 T 2 ) 2 . ( r 2 r 1 ) 3 = ( 28 365 ) 2 . ( 390 ) 3 ≈ 350.10 3 ( l ầ n )
Đáp án: A

Chọn B
Vận tốc dài của vệ tinh v = ωr = (2π/T).r
Lực hấp dẫn đóng vai trò là lực hướng tâm.
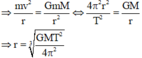
Thay T = 24h = 86400 s; M = 6.1024 kg, G vào → r = 42298 km

Lực hấp dẫn giữa Trái Đất và Mặt Trăng có độ lớn là:
F h d = G M m R 2 = 6 , 67.10 − 11 . 7 , 37.10 22 .6.10 24 ( 38.10 7 ) 2 = 2 , 04.10 20 N
Đáp án: A

- Chọn B.
Áp dụng công thức
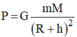
(h là khoảng cách từ vật tới mặt đất) ta được:
Tại mặt đất (h = 0):
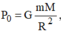
Tại độ cao h = R (cách tâm trái đất 2R), ta có:
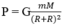
Lập tỷ lệ ta được:
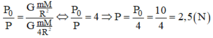
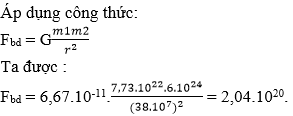
Chọn đáp án C
+ Áp dụng công thức: