Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Trong tam giác ABC vuông tại A, cạnh AC = b, ∠ (ACB) = α thì:
Khi b = 12 (cm), α = 42 ° thì
c = 12tg 42 ° ≈ 10,805 (cm), ∠ (ABC) = 48 ° , a = 12/(cos 42 ° ) ≈ 16,148 (cm).

Xét ΔABC vuông tại A có
\(AC=AB\cdot\tan60^0=3\sqrt{3}\simeq5,1962\left(cm\right)\)
=>\(BC=\sqrt{AB^2+AC^2}=6\left(cm\right)\)

Trong tam giác ABC vuông tại A, cạnh AC = b, ∠ (ABC) = β thì:

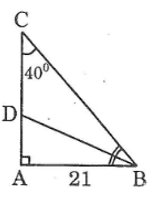
a) Ta có: \(AC=AB.\cot\widehat{C}=21.\cot\widehat{40^o}\simeq25,0268\left(cm\right)\)
b) Ta có: \(BC=\dfrac{AC}{\sin\widehat{C}}=\dfrac{21}{\sin\widehat{40^o}}\simeq32,6702\left(cm\right)\)
c) Vì ΔABCΔABC vuông tại A nên \(\widehat{B}+\widehat{C}=90^o\)
Suy ra: \(\widehat{B}=90^o-\widehat{C}=90^o-40^o=50^o\)
Vì BD là phân giác của B nên:
\(\widehat{ABD}=\dfrac{1}{2}\widehat{B}=\dfrac{1}{2}.50^o=25^o\)
Trong tam giác vuông ABD, ta có:
\(BD=\dfrac{AB}{\cos\widehat{ABD}}=\dfrac{21}{\cos25^o}\simeq23,1709\left(cm\right)\)

giả sử góc a=135 độ , thì góc d=45 độ.kẻ đường cao ah khi đó góc dah=45 độ vậy tam giác adh cân và vuông.áp dụng pytago ah=6.căn bậc hai của 2.vậy diện tích hbh=15.6 căn bậc 2 của 2=90.căn bậc 2 của 2(cm^2)
vì ABCD là hình bình hành
=> AD // BC ( tính chất )
=> \(\widehat{A}+\widehat{B}=180^0\)( hai góc trong cùng phía)
=> \(\widehat{B}=180^0-110^0=70^0\)
Kẻ AH\(\perp\)BC tại H, ta có tam giác vuông ABH
Xét tam giác vuông ABH, có:
AH=AB*sin B=12*sin 70 độ
\(AH\approx11,276\)(cm)
ta có: AD=BC ( ABCD là hình chữ nhật )
\(\Rightarrow S_{ABCD}=AH\cdot BC\approx11,276\cdot15=169,14\)(\(cm^2\))

b: XétΔADE vuông tại E có \(AE=AD\cdot\cos A\)
nên AE=5,16(cm)
AB=AE-BE=2,66(cm)


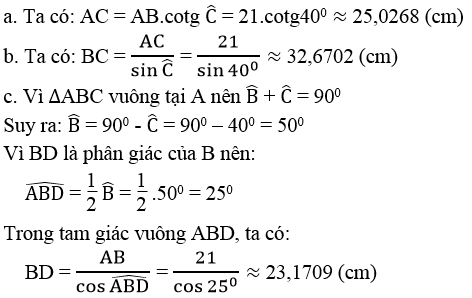
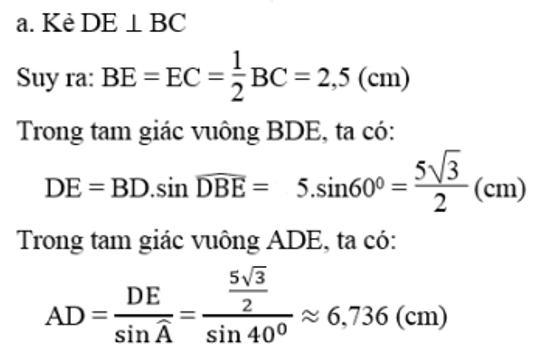
Trong tam giác ABC vuông tại A, cạnh AC = b, ∠ (ABC) = β thì: