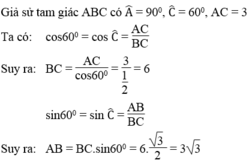Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

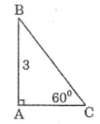
Xét ΔABC vuông tại A có
\(AC=AB\cdot\tan60^0=3\sqrt{3}\simeq5,1962\left(cm\right)\)
=>\(BC=\sqrt{AB^2+AC^2}=6\left(cm\right)\)

Trong tam giác ABC vuông tại A, cạnh AC = b, ∠ (ACB) = α thì:
Khi b = 12 (cm), α = 42 ° thì
c = 12tg 42 ° ≈ 10,805 (cm), ∠ (ABC) = 48 ° , a = 12/(cos 42 ° ) ≈ 16,148 (cm).

Trong tam giác ABC vuông tại A, cạnh AC = b, ∠ (ABC) = β thì:


Gọi độ dài của tam giác vuông là x. Điều kiện x > 0.
Tỉ số giữa cạnh huyền và một cạnh góc vuông sẽ là x/15.
Theo bài ra ta có :
x/15=13/12 (=) 12x=13*15 (=) 12x = 195 (=) x=16,25
Vậy độ dài cạnh huyền là 16,25 cm