
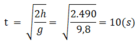
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

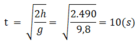

Gọi v 0 là tốc độ của gói hàng khi rời khỏi máy bay. Ta có:
L m a x = v 0 t = 150.10 = 1500 m.

Qũy đạo bay của gói hàng: \(y=\dfrac{g}{2v_0^2}x^2\)
Thời gian rơi: \(t=\sqrt{\dfrac{2h}{g}}=\sqrt{\dfrac{2\cdot490}{10}}=7\sqrt{2}s\)
Tầm bay xa: \(L=v_0t=180\cdot7\sqrt{2}=1781,91m\)
Vận tốc: \(v=\sqrt{\left(gt\right)^2+v_0^2}=\sqrt{\left(10\cdot7\sqrt{2}\right)^2+180^2}=10\sqrt{422}\)m/s

Trong trường hợp khí cầu đang bay lên thì lúc đầu vật được ném lên cao với vận tốc đầu v 0 = 4,9 m/s bằng vận tốc bay lên của khí cầu từ độ cao s và chuyển động chậm dần đều trong khoảng thời gian t 2 lên tới độ cao lớn nhất, tại đó v = 0. Khoảng thời gian t 2 được tính theo công thức:
v = v 0 – g t 2 = 0 ⇒ t 2 = 0,5 s
Sau đó vật lại rơi tự do từ độ cao lớn nhất xuống đến độ cao 300 m trong thời gian t 2 = 0,5 s, rồi tiếp tục tơi nhanh dần đều với vận tốc v 0 = 4,9 m/s từ độ cao 300 m xuống tới đất trong khoảng thời gian t 1 ≈ 7,3 s (giống như trường hợp trên).
Như vậy, khoảng thời gian chuyển động của vật sẽ bằng: t = 2 t 2 + t 1 = 2.0,5 + 7,3 = 8,3 s.

Khi gói hàng chạm đất, y= 0, chọn gốc tại mặt đất
\(y=h+v_{0y}t-\frac{1}{2}gt^2\)
\(\Leftrightarrow490+150.\sin\alpha.t-\frac{1}{2}.9,8.t^2=0\)
\(\Leftrightarrow490-4,9t^2=0\Leftrightarrow t=10\left(s\right)\)
\(x=v_{0x}.t=150.\cos\alpha.t=150.10=1500\left(m\right)\)

Trong trường hợp khí cầu đang hạ xuống thì vật rơi nhanh dần đều với vận tốc đầu v 0 = 4,9 m/s bằng vận tốc hạ xuống của khí cầu từ độ cao s được tính theo công thức s = v 0 t + (g t 2 )/2
Thay số vào ta thu được phương trình bậc 2:
300 = 4.9t + (9.8 t 2 )/2 ⇔ t 2 + t - 300/4.9 = 0
Giải ra ta tìm được t ≈ 7,3 s (chú ý chỉ lấy nghiệm t > 0)
Như vậy thời gian rơi của vật là t ≈ 7,3 s

Ta có:
v0 = 500 km/h = 138,89 m/s
h = 5 km = 5000 m
Người lái máy bay phải thả vật cách mục tiêu là: \(L = {v_0}.\sqrt {\frac{{2h}}{g}} = 138,89.\sqrt {\frac{{2.5000}}{{9,8}}} \approx 4436,68(m)\)