Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương pháp: sử dụng pp động lực học
Cách giải:
Tần số góc là
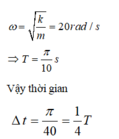
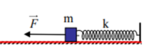
Vật chịu tác dụng của ngoại lực F đến vị trí cân bằng thì thôi tác dụng lực
Theo định luật II Niu tơn ta có:
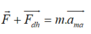
Vì F và lực đàn hồi cùng chiều nên ta có
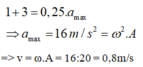
Đáp án C

Đáp án D
+ Tần số góc và chu kì của dao động ω = k m = 100 0 , 25 = 20 rad/s → T = 0,1π s.
Dưới tác dụng của lực F, vật sẽ dao động quanh vị trí cân bằng O′ cách vị trí lò xo không giãn O một đoạn O O ' = F k = 3 100 = 3 cm.
→ Thời điểm xảy ra biến cố vật có v = 0 → A = 1 + 3 = 4 cm.
+ Ta lưu ý rằng lực F chỉ tồn tại trong khoảng thời gian Δ t = T 4 = π 40 s vật đến vị trí cân bằng O′ thì lực F ngừng tác dụng, tốc độ của vật khi đó là v′ = ωA = 80 cm/s.
+ Khi không còn lực F tác dụng, vật sẽ dao động quanh vị trí cân bằng cũ O, vậy tại vị trí lực F ngừng tác dụng thì li độ của vật so với vị trí cân bằng cũ là x′ = 3 cm, v = 80 cm → A ' = x 2 + v 0 ω 2 = 3 2 + 80 20 2 = 5 cm.
→ Tốc độ cực đại của vật v ' m a x = ω A ′ = 100 c m / s .

Đáp án D
+ Tần số góc và chu kì của dao động ω = k m = 100 0 , 25 = 20 rad/s → T = 0,1π s.
Dưới tác dụng của lực F, vật sẽ dao động quanh vị trí cân bằng O′ cách vị trí lò xo không giãn O một đoạn O O ' = F k = 3 100 = 3 cm.
→ Thời điểm xảy ra biến cố vật có v = 0 → A = 1 + 3 = 4 cm.
+ Ta lưu ý rằng lực F chỉ tồn tại trong khoảng thời gian Δ t = T 4 = π 40 s vật đến vị trí cân bằng O′ thì lực F ngừng tác dụng, tốc độ của vật khi đó là v′ = ωA = 80 cm/s.
+ Khi không còn lực F tác dụng, vật sẽ dao động quanh vị trí cân bằng cũ O, vậy tại vị trí lực F ngừng tác dụng thì li độ của vật so với vị trí cân bằng cũ là x′ = 3 cm, v = 80 cm → A ' = x 2 + v 0 ω 2 = 3 2 + 80 20 2 = 5 cm.
→ Tốc độ cực đại của vật v ' m a x = ω A ′ = 100 c m / s .

Tần số góc: \(\omega=\sqrt{\frac{K}{m}}=10\pi\left(rad\text{/}s\right)\)
Biên độ dao động của vật \(A=\sqrt{x^2+\left(\frac{v}{w}\right)^2}=6\left(cm\right)\)
Lò xo có độ nén cực đại tại biên âm:
\(\Rightarrow\) Góc quét \(=\pi\text{/}3+\pi=\omega t\Rightarrow t=2\text{/}15\left(s\right)\)
chọn B

Khoảng thời gian giữa 2 lần liên tiếp động ăng bằng thế năng là T/4
\(\Rightarrow \dfrac{T}{4}=\dfrac{\pi}{40}\)
\(\Rightarrow T = \dfrac{\pi}{10}\)
\(\Rightarrow \omega=\dfrac{2\pi}{T}=20(rad/s)\)
Biên độ dao động: \(A=\dfrac{v_{max}}{\omega}=\dfrac{100}{20}=5(cm)\)
Ban đầu, vật qua VTCB theo chiều dương trục toạ độ \(\Rightarrow \varphi=-\dfrac{\pi}{2}\)
Vậy PT dao động là: \(x=5\cos(20.t-\dfrac{\pi}{2})(cm)\)

Độ biến dạng của lò xo khi vật ở VTCB là: \(\Delta \ell_0=\dfrac{mg}{k}=\dfrac{1.10}{100}=0,1m=10cm\)
\(\omega=\sqrt{\dfrac{k}{m}}=10(rad/s)\)
Áp dụng CT: \(A^2=x^2+\dfrac{v^2}{\omega^2}\)
\(\Rightarrow A^2=2^2+\dfrac{(20\sqrt 3)^2}{10^2}\)
\(\Rightarrow A = 4cm\)
Lực đàn hồi cực đại:
\(F_{dhmax}=k\Delta\ell_{max}=k(\Delta\ell_0+A)=100.(0,1+0,04)=14(N)\)
Lực đàn hồi cực tiểu:
\(F_{dhmin}=k\Delta\ell_{min}=k(\Delta\ell_0-A)=100.(0,1-0,04)=6(N)\)

Do vật không chịu tác dụng của lực ma sát, nên cơ năng không đổi,
Khi chịu tác dụng lực thì vật dao động quanh vị trí cân bằng O’ mới. khi ngứng tác dụng lực thì vị trí và vận tốc tại thời điểm đó thay đổi, vị trí cân bằng trở lại vị trí cũ, nhưng cơ năng bảo toàn nên vận tốc cực đại vẫn như cũ
Đáp án C

\(A=l'=\frac{mg}{k}=\frac{g}{\omega^2}\)
\(v_0=A\omega\Rightarrow\frac{g}{\omega}=v_0\Rightarrow\omega=\frac{g}{v_0}\)
\(\Rightarrow A=\frac{g}{\omega^2}=\frac{v^2_0}{g}=6,25\left(cm\right)\)
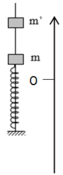
Giải thích: Đáp án D
Phƣơng pháp: Sử dụng hệ thức độc lập theo thời gian của x và v
Cách giải:
- Nếu không tác dụng lực vật sẽ dao động với biên độ A1 = 1 cm
- Khi có lực tác dụng VTCB dịch đi theo hướng lực tác dụng đoạn
- Nên ngay khi thả vật sẽ dao động với biên độ A2 = A1 + x0 = 4 cm
- Chu kì dao động của vật là: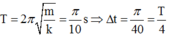
- Sau khi thả vật đi đến VTCB O1, lúc này vật có vận tốc là v2max = ωA2 = 80 cm/s
- Lúc này mất lực nên VTCB lại về O => lúc này vật có li độ là x = 3 cm nên dao động với biên độ là:
Chọn D