Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Tần số góc của dao động ω = k m = 10 rad/s → T = 0,2 s.
→ Tốc độ của vật khi đi qua vị trí cân bằng v = v m a x = ω A = 20 3 cm/s.
+ Dưới tác dụng của ngoại lực con lắc dao động quanh vị trí cân bằng mới O′, tại vị trí này lò xo giãn một đoạn O O ' = Δ l 0 = F k = 2 100 = 2 cm.
+ Tại ví trí xuất hiện ngoại lực, con lắc có x ' = - 2 cm, v ' = v m a x
→ Biên độ dao động của con lắc lúc này A 1 = x ' 2 + v ' ω = 2 2 + 20 3 10 2 = 4 cm.
+ Ta chú ý rằng con lắc dao động quanh vị trí cân bằng mới O′ trong khoảng thời gian Δ t = T 6 = 1 30 s, sau khoảng thời gian này, vật có x 1 = 0 , 5 A 1 , v 1 = 3 v 1 m a x 2 = 3 ω A 1 2 = 3 10 π .4 2 = 20 3 π cm/s.
→ Ngừng lực tác dụng F, con lắc lại dao động quanh vị trí cân bằng cũ, lúc này con lắc có x ′ = O O ′ + 0 , 5 A 1 = 4 c m , v ' = v 1 = 20 3 π cm/s.
→ Biên độ dao động mới A 2 = x ' 2 + v ' ω 2 = 4 2 + 20 3 π 10 π 2 = 2 7 cm.
→ Vậy A 1 A 2 = 4 2 7 = 2 7

Đáp án B
Khi chưa có lực F , vị trí cân bằng của vật là O . Biên độ là : A = 2 3 c m
Khi có thêm lực F, vị trí cân bằng dịch chuyển đến O’ sao cho : OO' = F k = 0 , 02 m = 2 c m
ω = k m = 10 π rad / s ⇒ T = 0 , 2 s
Khi F bắt đầu tác dụng (t=0), vật đến O có li độ so với O’ là : x 1 = - 2 c m và có vận tốc v 1 = ω A = 20 π 3 cm / s
Biên độ : A 1 = x 1 2 + v 1 ω 2 = 4 c m
Thời gian ngắn nhất vật đi từ O đến O’ là: t 1 = T 60 = 1 60 s
Ta thấy rằng t = 1 30 s = 2 t 1 nên khi F ngừng tác dụng thì vật có li độ so với O là x 2 = 4 c m và có vận tốc v 2 = v 1 = ω A = 20 π 3 cm / s
Từ đó biên độ từ lúc ngừng tác dụng lực là :
A 2 = x 2 2 + v 2 ω 2 = 2 7 c m
Vậy A 1 A 2 = 2 7

Khoảng thời gian giữa 2 lần liên tiếp động ăng bằng thế năng là T/4
\(\Rightarrow \dfrac{T}{4}=\dfrac{\pi}{40}\)
\(\Rightarrow T = \dfrac{\pi}{10}\)
\(\Rightarrow \omega=\dfrac{2\pi}{T}=20(rad/s)\)
Biên độ dao động: \(A=\dfrac{v_{max}}{\omega}=\dfrac{100}{20}=5(cm)\)
Ban đầu, vật qua VTCB theo chiều dương trục toạ độ \(\Rightarrow \varphi=-\dfrac{\pi}{2}\)
Vậy PT dao động là: \(x=5\cos(20.t-\dfrac{\pi}{2})(cm)\)

Gọi biên độ dao động là A.
Độ dãn của lò xo khi vật ở VTCB là: \(\Delta\ell_0=\dfrac{mg}{k}\)
Độ dãn cực đại của lò xo là: \(\Delta\ell_0+A=10cm=0,1m\)
Lực đàn hồi cực tiểu là: \(k(\Delta\ell_0-A)=0,8\)
\(\Rightarrow k(\Delta \ell_0+\Delta\ell_0-0,1)=0,8\)
\(\Rightarrow k(2\Delta \ell_0-0,1)=0,8\)
\(\Rightarrow k(2\dfrac{mg}{k}-0,1)=0,8\)
\(\Rightarrow2.mg-0,1.k=0,8\)
\(\Rightarrow2.0,24.10-0,1.k=0,8\)
\(\Rightarrow k=40(N/m)\)
Lực mà lò xo tác dụng lên vật khi lò xo dãn 5cm là lực đàn hồi của lò xo và bằng: \(F=k.\Delta\ell=40.0,05=2(N)\)

+ Tại vị trí lực đàn hồi của lò xo bằng 12 N ta có:
F d h = m g + k x → k x = 12 − 1.10 = 2 = F k v với x chính là biên độ dao động của vật.
+ Mặc khác: k . Δ l = m g = 10 > k A
® Δ l > A
® Lực đàn hồi nhỏ nhất tác dụng lên vật là: F d h min = k Δ l − A = k Δ l − k A = 10 − 2 = 8 N
Đáp án C

Chọn B
+ Gọi ΔA là độ giảm biên độ mỗi lần vật qua vị trí cân bằng.
![]()
![]()
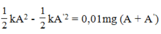
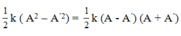
![]()
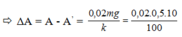
![]()
+ Vậy số lần vật qua vị trí cân bằng là N = A/ΔA = 50.

Tần số góc: \(\omega=\sqrt{\frac{K}{m}}=10\pi\left(rad\text{/}s\right)\)
Biên độ dao động của vật \(A=\sqrt{x^2+\left(\frac{v}{w}\right)^2}=6\left(cm\right)\)
Lò xo có độ nén cực đại tại biên âm:
\(\Rightarrow\) Góc quét \(=\pi\text{/}3+\pi=\omega t\Rightarrow t=2\text{/}15\left(s\right)\)
chọn B

Do vật không chịu tác dụng của lực ma sát, nên cơ năng không đổi,
Khi chịu tác dụng lực thì vật dao động quanh vị trí cân bằng O’ mới. khi ngứng tác dụng lực thì vị trí và vận tốc tại thời điểm đó thay đổi, vị trí cân bằng trở lại vị trí cũ, nhưng cơ năng bảo toàn nên vận tốc cực đại vẫn như cũ
Đáp án C
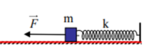
Đáp án A
- Vị trí cân bằng mới O’ cách vị trí cân bằng đầu là a = 2 (cm)
- Khi tác dụng lực F thì biên độ dao động của vật là A1 = 4 (cm)
- Khi thôi tác dụng lực F thì khi đó li độ của vật theo gốc O’ là 2(cm) nên li độ theo gốc O là 4cm, khi đó vận tốc của vật là
- Biên độ của vật khi thôi tác dụng lực F là
Do vậy tỉ số
Nhận xét: Bài toán này cùng lớp với một bài toán phân loại trong đề thi Đại học Khối A năm 2013