Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Con lắc lò xo dao động với chiều dài cực đại là 38 cm → A = 38 – 30 = 8 c m .
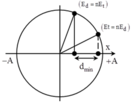
+ Vị trí động năng của vật bằng n lần thế năng: E d = n E t E d + E t = E → x = ± A n + 1
+ Tương tự như vậy vị trí vật có thế năng bằng n lần động năng tại x = ± n n + 1 A
→ Từ hình vẽ ta thấy:
d min = A n n + 1 − 1 n + 1 = 4 → S h i f t → S o l v e n ≈ 5
ü Đáp án B

Đáp án B
+ Biên độ của dao động A = l m a x – l 0 = 38 – 30 = 8 c m .
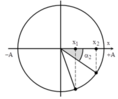
Vị trí động năng bằng n lần thế năng x 1 = ± A n + 1
Vị trí thế năng bằng n lần động năng x 2 = ± n n + 1 A
Ta có A = A cos α 2 – A cos 1
→ Hay S = A n n + 1 − A 1 n + 1 → n = 4,9.

+ Biên độ dao động: l max = l 0 + A ⇒ A = l − l 0 = 8 c m
+ Vị trí W d = n W t ( c h ỉ l ấ y x > 0 ) x = A n + 1
+ Vịu trí W t = n W đ (hay W d = 1 n W t ): x = A 1 n + 1 = A n n + 1
+ Theo đề bài ta có: x 1 − x 2 = 4 ⇒ A n − 1 n + 1 = 4 ⇒ n − 1 n + 1 = 1 2 ⇒ n = 4 , 9
Chọn đáp án C

Đáp án C
Biên độ dao động: lmax = l0 + A => A = l - l0 = 8 cm
Vị trí Wd = nWt (chỉ lấy x > 0): x = A n + 1
Vị trí Wt = nWd hay W d = 1 n W t : x = A 1 n + 1 = A n n + 1
Theo đề bài ta có:

Cơ năng: \(W=0,064+0,096=0,16J\) \(\Rightarrow v_{max}=\sqrt{3,2}\)(m/s)
+ Thời điểm t1: \(v_1=\sqrt{1,92}\)(m/s)
+ Thời điểm t2: \(v_2=\sqrt{1,28}\)(m/s)
Biểu diễn sự biến thiên vận tốc bằng véc tơ quay ta có:
√3,2 √1,28 √1,92 v O M N
Do \(v_1^2+v_2^2=v_{max}^2\) nên OM vuông góc ON.
Như vậy góc quay là \(90^0\)
Thời gian: \(t=\frac{1}{4}T=\frac{\pi}{48}\Rightarrow T=\frac{\pi}{12}\)
\(\Rightarrow\omega=24\)(rad/s)
Biên độ: \(A=\frac{v_{max}}{\omega}=\frac{\sqrt{3,2}}{24}=0,07m=7cm\)
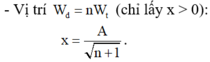
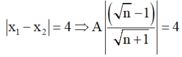
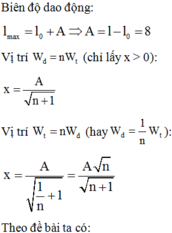
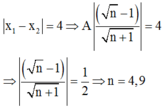

Đáp án B
+ Ta có :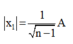
ở vị trí mà động năng bằng n lần thế năng :
ở vị trí mà thế năng bằng n lần động năng :
+ Khoảng cách ngắn nhất khi x 1 , x 2 cùng dấu khi đó :