Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Nối các điểm ta có tứ giác MNPQMNPQ
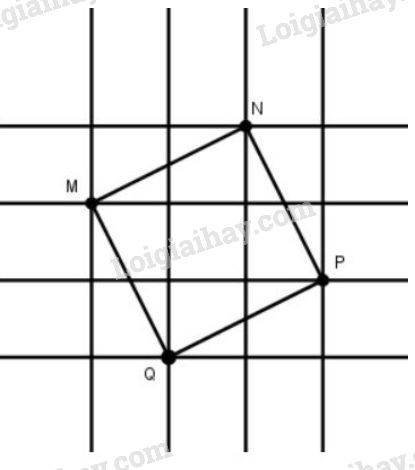
Tứ giác MNPQMNPQ có:
- Các cạnh bằng nhau và cùng bằng đường chéo của hình chữ nhật có chiều dài 2cm2cm, chiều rộng 1cm1cm. Do đó theo định lí Py-ta-go, ta có:
MN=NP=PQ=QM=√22+12=√5(cm)MN=NP=PQ=QM=22+12=5(cm).
Hay MNPQMNPQ là hình thoi.
- Các đường chéo bằng nhau và cùng bằng đường chéo của hình chữ nhật có chiều dài 3cm3cm, chiều rộng 1cm1cm nên theo định lý Py-ta-go ta có độ dài đường chéo là:
MP=NQ=√32+12=√10(cm).MP=NQ=32+12=10(cm).
Như vậy hình thoi MNPQMNPQ có hai đường chéo bằng nhau nên MNPQMNPQ là hình vuông.
Vậy diện tích hình vuông MNPQMNPQ bằng MN2=(√5)2=5(cm2)
Ta thấy mỗi cạnh của tứ giác MNPQMNPQ là đường chéo của hình chữ nhật do hai ô vuông ghép lại, nên hình đó có bốn cạnh bằng nhau và bằng \sqrt{1^2+2^2}=\sqrt{5}căn 1^2 + 2^2 = căn 5 (đvđd) (định lý Pytago)
Tứ giác MNPQMNPQ có bốn cạnh bằng nhau nên tứ giác MNPQMNPQ là hình thoi.
Mỗi đường chéo của tứ giác MNPQMNPQ là đường chéo của hình chữ nhật do ba ô vuông ghép lại, nên giác MNPQMNPQ có hai đường chéo bằng nhau và bằng căn 1^ 2 + 3^2 = căn 10 đvđ d\sqrt{1^2+3^2}=\sqrt{10}c(đvđd)
Hình thoi MNPQMNPQ có hai đường chéo bằng nhau nên tứ giác MNPQMNPQ là hình vuông.
Diện tích hình vuông MNPQMNPQ:
S = (\sqrt{5})^2 = 5S=(căn5)^22 =5 (đvdt)

Dựa vào định lý Pitago, ta thấy mỗi cạnh của tứ giác MNPQ là đường chéo của hình chữ nhật do hai ô vuông ghép lại, nên hình đó có bốn cạnh bằng nhau và bằng
![]()
Tứ giác MNPQ là hình thoi có bốn cạnh bằng nhau.
Mỗi đường chéo của tứ giác MNPQ là đường chéo của hình chữ nhật do ba ô vuông ghép lại, nên giác NMPQ có hai đường chéo bằng nhau và bằng
![]()
Hình thoi MNPQ là hình vuông có hai đường chéo bằng nhau.
Diện tích hình vuông MNPQ:
S = ( √ 5 ) 2 = 5 ( c m 2 )

cái hình thì mk gửi link trong ib nhé
a) Gọi O là giao điểm của AC và BD
\(\Delta OAB\) vuông tại O có \(OA^2+OB^2=AB^2=49\)
Lại có: \(\tan BAC=\tan OAB=\frac{OB}{OA}=\frac{3}{4}\)\(\Leftrightarrow\)\(\frac{OA^2}{16}=\frac{OB^2}{9}=\frac{OA^2+OB^2}{16+9}=\frac{49}{25}\)
\(\Rightarrow\)\(\hept{\begin{cases}\frac{OA}{4}=\frac{7}{5}\\\frac{OB}{3}=\frac{7}{5}\end{cases}}\Leftrightarrow\hept{\begin{cases}OA=\frac{28}{5}\left(cm\right)\\OB=\frac{21}{5}\left(cm\right)\end{cases}}\)
\(\Rightarrow\)\(\hept{\begin{cases}AC=2OA=\frac{56}{5}\left(cm\right)\\BD=2OB=\frac{42}{5}\left(cm\right)\end{cases}}\)
\(\Rightarrow\)\(S_{ABCD}=\frac{1}{2}AC.BD=\frac{1}{2}.\frac{56}{5}.\frac{42}{5}=\frac{1176}{25}=47,04\left(cm^2\right)\)
b) Gọi E, F lần lược là giao điểm của BD với MN và PQ
tam giác ABD có MQ // BD
\(\Rightarrow\)\(\frac{MQ}{BD}=\frac{MA}{AB}\) ( hệ quả định lí Talet )
tam giác OAD có QF // OA
\(\Rightarrow\)\(\frac{QF}{OA}=\frac{DQ}{AQ}=\frac{MB}{AB}\) ( hệ quả định lí Talet )
\(\Rightarrow\)\(\frac{MQ}{BD}+\frac{QF}{OA}=\frac{MA+MB}{AB}=1\)
\(\Rightarrow\)\(1\ge2\sqrt{\frac{MQ.QF}{BD.OA}}\)\(\Leftrightarrow\)\(MQ.QF\le\frac{1}{4}BD.OA\)
Tương tự, ta cũng có: \(NP.PF\le\frac{1}{4}BD.OC\)
\(\Rightarrow\)\(MQ.QF+NP.PF=S_{MEFQ}+S_{NEFP}=S_{MNPQ}\le\frac{1}{4}BD.AC=\frac{1}{2}S_{ABCD}=23,52\left(cm^2\right)\)
Dấu "=" xảy ra khi M, N, P, Q là trung điểm của AB, BC, CD, DA

đặt MA= x (cm)
tam giác ABC cân nên : 12-x
diện tích hình bình hành MNCP là : MP.MA = (12-x)x
diện tích bằng 32cm vuông , nê ta có phương trình:
x^2 -12x +32 = 0
giải pt ta được x1= 4 , x2 =8
vậy M cách A là 4cm hoặc 8cm.

Có hình vẽ : A B C D H K o
Dễ thấy SABCD = \(\frac{1}{2}\left(AH+CK\right).BD\)
mà lại có \(AH=AO.sin\alpha\) ; \(CK=OC.sin\alpha\)
=> SABCD = \(\frac{1}{2}\sin\alpha.AC.BD\)
Khi 2 đường chéo vuông góc với nhau thì
\(H\equiv O\equiv K\Rightarrow AH=AO=CK\)
hay \(sin\alpha=1\)
Khi đó \(S_{ABCD}=\frac{1}{2}mn\)(đpcm)



Dựa vào định lý Pitago, ta thấy mỗi cạnh của tứ giác MNPQ là đường chéo của hình chữ nhật do hai ô vuông ghép lại, nên hình đó có bốn cạnh bằng nhau và bằng
Tứ giác MNPQ là hình thoi có bốn cạnh bằng nhau.
Mỗi đường chéo của tứ giác MNPQ là đường chéo của hình chữ nhật do ba ô vuông ghép lại, nên giác NMPQ có hai đường chéo bằng nhau và bằng
Hình thoi MNPQ là hình vuông có hai đường chéo bằng nhau.
Diện tích hình vuông MNPQ:
S = (√5)2 = 5 (cm2)