Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

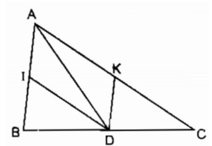
Ta có: DK // AB (gt)
hay DK // AI
DI // AC (gt)
hay DI // AK
Vậy tứ giác AIDK là hình bình hành

a) Học sinh tự chứng minh
b) nếu AEDF là hình thoi thì AD là phân giác của F A E ^ suy ra AD là phân giác của B A C ^

a) Tứ giác AEDF là hình bình hành.
Vì có DE // AF, DF // AE (gt) (theo định nghĩa)
b) Hình bình hành AEDF là hình thoi khi AD là tia phân giác của góc A. Vậy nếu D là giao điểm của tia phân giác góc A với cạnh BC thì AEDF là hình thoi.
.

a) Xét tứ giác AEDF có
FD//AE(gt)
AF//DE(gt)
Do đó: AEDF là hình bình hành(Dấu hiệu nhận biết hình bình hành)

Dễ Thui
Hình vẽ
A B C D E F
Vì DE song song với AC nên
Theo định lí Ta lét
Ta có
\(\frac{AE}{AB}=\frac{CD}{BC}\)
Vì DF song song với AB nên
Theo định lí Ta lét
Ta có: \(\frac{AF}{AC}=\frac{BD}{BC}\)
Suy ra \(\frac{AE}{AB}+\frac{AF}{AC}=\frac{CD}{BC}+\frac{BD}{BC}=\frac{BC}{BC}=1\)
Vậy ...........................

Để hình bình hành AIDK là hình thoi.
⇒ AD là đường phân giác của ∠ (IAK)
hay AD là đường phân giác của ∠ (BAC)
Ngược lại nếu AD là tia phân giác của ∠ (BAC)
Ta có tứ giác AIDK là hình bình hành có đường chéo AD là phân giác của góc A nên tứ giác AIDK là hình thoi
Vậy hình bình hành AIDK là hình thoi khi và chỉ khi D là giao điểm tia phân giác của góc A và cạnh BC.