Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

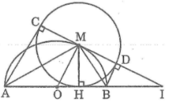
Trong đường tròn (M; MH), theo tính chất hai tiếp tuyến cắt nhau, ta có:
AC = AH và BD = BH
Khi M thay đổi trên nửa đường tròn tâm O thì AC luôn bằng AH và BD luôn bằng BH
Suy ra: AC + BD = AH + BH = AB không đổi

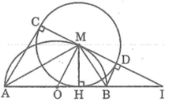
Trong đường tròn (M; MH), theo tính chất hai tiếp tuyến cắt nhau, ta có:
- MA là tia phân giác của góc HMC

Vậy C, M, D thẳng hàng.

A B M H O C D I
a) Áp dụng tính chất hai tiếp tuyến giao nhau: ^HMC = 2.^AMH; ^HMD = 2.^BMH
Suy ra ^HMC + ^HMB = 2(^AMH + ^BMH) = 1800 => 3 điểm C,M,D thẳng hàng (đpcm).
Có C,M,D thẳng hàng, Do C,D thuộc (M;MH) nên CD là đường kính của (M;MH)
Khi đó MO là đường trung bình của hình thang vuông ACDB => MO // AC // BD
=> MO vuông góc CD => CD là tiếp tuyến của (O) (đpcm).
b) Dễ thấy AC + BD = AH + BH = 2R (R là bán kính của (O)) (không đổi).
c) Áp dụng hệ thức lượng trong tam giác vuông IMO có OH.OI = OM2 = R2 (không đổi).

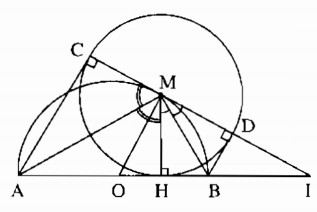
Ta có: AC ⊥ CD và BD ⊥ CD (tính chất tiếp tuyến)
Suy ra: AC // BD hay tứ giác ABDC là hình thang
Mà OA = OB (bán kính (O))
Và AC = MD (bán kính (M))
Suy ra OM là đường trung bình của hình thang ABDC
Khi đó OM // AC. Suy ra: OM ⊥ CD hay góc (OMI) = 90 °
Tam giác OMI vuông tại M có MH ⊥ OI
Theo hệ thức lượng trong tam giác vuông ta có: O M 2 = OH.OI
Suy ra: OH.OI = R 2 không đổi.