Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. Dây đi qua M ngắn nhất là dây AB vuông góc với OM
Áp dụng định lí Pitago vào tam giác vuông OAM ta có:
OA2 = AM2 + OM2
Suy ra: AM2 = OA2 – OM2 = 52 – 32 = 16
AM = 4 (dm)
Ta có: OM ⊥ AB
Suy ra: AM = (\(\frac{1}{2}\)).AB
Hay: AB = 2AM = 2.4 = 8 (dm)
b. Dây đi qua M lớn nhất khi nó là đường kính của đường tròn (O). Vậy dây có độ dài bằng 2R = 2.5 = 10 (dm)
a. Dây đi qua M ngắn nhất là dây AB vuông góc với OM
Áp dụng định lí Pitago vào tam giác vuông OAM ta có:
OA2 = AM2 + OM2
Suy ra: AM2 = OA2 – OM2 = 52 – 32 = 16
AM = 4 (dm)
Ta có: OM ⊥ AB
Suy ra: AM = (\(\frac{1}{2}\)).AB
Hay: AB = 2AM = 2.4 = 8 (dm)
b. Dây đi qua M lớn nhất khi nó là đường kính của đường tròn (O). Vậy dây có độ dài bằng 2R = 2.5 = 10 (dm)

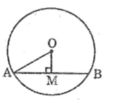
Dây đi qua M ngắn nhất là dây AB vuông góc với OM
Áp dụng định lí Pitago vào tam giác vuông OAM ta có:
O A 2 = A M 2 + O M 2
Suy ra: A M 2 = O A 2 - O M 2 = 5 2 - 3 2 = 16
AM = 4 (dm)
Ta có: OM ⊥ AB
Suy ra: AM = (1/2).AB
Hay: AB = 2AM = 2.4 = 8 (dm)

O M M' A B
a) Giả sử dây AB bất kì đi qua M. Ta kẻ \(OM'\perp AB\) (M' thuộc AB)
Xét trong tam giác OMM' , ta có : \(OM\ge OM'\)(quan hệ giữa đường xiên và hình chiếu)
Do đó : dây AB dài nhất \(\Leftrightarrow AB\perp OM\)
Vậy dây ngắn nhất vuông góc với bán kính đi qua M
Tới đây áp dụng đ/l Pytago là ra...
b) Dây dài nhất là dây đi qua tâm...
O A M B
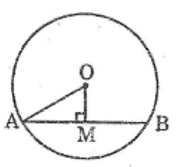
a) Dây đi qua M ngắn nhất là dây AB vuông góc với OM
Áp dụng định lí Pitago vào tam giác vuông OAM ta có :
OA2 = AM2 + OM2
Suy ra: AM2 = OA2 – OM2 = 52 – 32 = 16
AM = 4 ( dm )
Ta có: \(OM\perp AB\)
Suy ra: \(AM=\left(\frac{1}{2}\right).AB\)
Hay: AB = 2AM = 2 . 4 = 8 ( dm )
b. Dây đi qua M lớn nhất khi nó là đường kính của đường tròn (O)
Vậy dây có độ dài bằng
2R = 2 . 5 = 10 ( dm )

Gọi dây đi qua M là AB. Kẻ OH vuông góc AB tại H.
Có MB AB≤2R=10
và OM≥OHOM≥OH quan hệ đường vuông góc và đường xiên.
vậy OH có giá trị lớn nhất bằng OM, khi đó độ dài dây AB nhỏ nhất = 8dm (liên hệ dây cung và khoảng cách đến tâm)
....... Từ đó suy ra kết quả.
a) Dây ngắn nhất đi qua M chính là dây vuông góc với bán kính.
Sau đó áp dụng đl Pytago là ra.
b) Dây dài nhất đi qua M chính là đường kính.

có AM=MC=AC/2=10 cm ; IB=IC= BC/2 ; mà AC=BC (tam giáccân)
----> AM=MC=IB=IC=10 cm
Kéo dài CO cắt AB tại D
tam giác AOC có OA=OC (bán kính)
--> tam giác AOC cân tại O có OM là trung tuyến
---> OM vuông góc AC hay góc OMC=90 o
Tương tự với tam giác OCB được OI vuông góc BC hay góc OIC=90 o
Xét tam giác vuông OMC và tam giác vuông OIC:
MC=IC=10cm OC cạnh chung
--->tam giác OMC = tam giác OIC (ch.cgv)
--> góc MCO= góc ICO
---> CO hay CD là phân giác góc ACB của tam giác cân ABC
---> CD vuông góc AB hay góc ADC=90 o
AD=BD=AB/2 = 12 cm
Theo Pytago trong tam giác ACD:
CD^ 2= AC^ 2 -AD ^2 = 20 ^2 -12^ 2 =256
---> CD=16 cm
Đặt OC=OA=X
--> OD= CD-OC = 16 - X
Theo Pytago tam giác AOD:
AO2= OD^ 2+AD^ 2
<-->X^ 2= (16-X)^ 2 + 12 ^2
<--> 16^ 2 -32X + X^ 2 +12^ 2 - X ^2=0
<--> 400 - 32X=0
<--> X= -400/-32= 12,5 cm
Vậy bán kính đường tròn bằng 12,5 cm

Trên BC lấy I sao cho IC=IB
Ta có AM=MC=AC/2=20/2= 10 cm
Từ M kẻ MH vuông góc AB. Theo gt, ta được MH=8 cm
Áp dụng Pytago trong tam giác vuông AMH: AH2= AM2 - MH2 = 102 - 82= 36 ----> AH=6 cm
có AM=MC ; IB=IC ---> MI=1/2AB=1/2 .24 =12 cm( đường TB)
Từ I kẻ IK vuông góc AB
có MI// AB( MI là đường trung bình) ; IK//MK (cùng vuông góc AB)
---> MIKH là hình bình hành
---> MI=HK=12 cm; MH=IK=8 cm
BK= AB-AH-HK = 24-6-12=6 cm
Xét tam giác AMH và tam giác BIK:
AH=BK=6
góc AHM= góc BKI= 90O
MH=IK=8
----> tam giác AMH=tam giác BIK(c.g.c)
----> góc MAH= góc IBK (cặp góc tương ứng) hay góc CAB= góc CBA
----> tam giác ABC cân tại C
b) có AM=MC=AC/2=10 cm ; IB=IC= BC/2 ; mà AC=BC (tam giáccân)
----> AM=MC=IB=IC=10 cm
Kéo dài CO cắt AB tại D
tam giác AOC có OA=OC (bán kính) --> tam giác AOC cân tại O
có OM là trung tuyến ---> OM vuông góc AC hay góc OMC=90o
Tương tự với tam giác OCB được OI vuông góc BC hay góc OIC=90o
Xét tam giác vuông OMC và tam giác vuông OIC:
MC=IC=10cm
OC cạnh chung
--->tam giác OMC = tam giác OIC (ch.cgv)
--> góc MCO= góc ICO ---> CO hay CD là phân giác góc ACB của tam giác cân ABC --->
- CD vuông góc AB hay góc ADC=90o
- AD=BD=AB/2 = 12 cm
Theo Pytago trong tam giác ACD: CD2= AC2-AD2 = 202-122 =256 ---> CD=16 cm
Đặt OC=OA=X --> OD= CD-OC = 16 - X
Theo Pytago tam giác AOD: AO2= OD2+AD2
<-->X2= (16-X)2 + 122
<--> 162 -32X + X2 +122 - X2=0
<--> 400 - 32X=0
<--> X= -400/-32= 12,5 cm
Vậy bán kính đường tròn bằng 12,5 cm
tại sao bạn không kẻ đường cao CD. Như thế sẽ đỡ mất thời gian chứng minh
Dây đi qua M lớn nhất khi nó là đường kính của đường tròn (O). Vậy dây có độ dài bằng 2R = 2.5 = 10 (dm)