Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Cạnh đáy của khối tám mặt là a 2 + a 2 2 = a 2 2 ⇒ diện tích đáy của khối tám mặt là:
S = a 2 2 2 = a 2 2
Thể tích của khối tám mặt là: V = 2. 1 3 . a 2 . a 2 2 = a 3 6

Chọn D
Tính độ dài một cạnh của hình lập phương theo a bằng cách sử dụng định lý Ta-lét

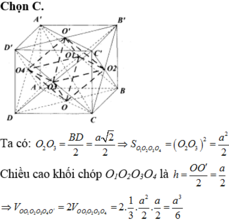
Chọn C.
Phương pháp:
Thể tích khối lập phương cạnh a là : V = a 3
Cách giải:
Khối lập phương có các đỉnh lần lượt là trọng tâm các mặt của khối bát diện đều cạnh a có độ dài cạnh là
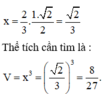

Đáp án D
Khối lập phương có các đỉnh lần lượt là trọng tâm các mặt của khối bát diện đều cạnh a có độ dài cạnh bằng x = 2 3 . a 2 2 = a 2 3 . Vậy thể tích cần tính là V = x 3 = 2 a 3 3 = 8 a 3 27

vì (C) đi qua điểm A nên tọa độ điểm A thỏa mãn pt \(y=\frac{ax^2-bx}{x-1}\) ta có \(\frac{5}{2}=\frac{a+b}{-2}\Rightarrow a+b=-5\)
vì tiếp tuyến của đồ thị tại điểm O có hệ số góc =-3 suy ra y'(O)=-3
ta có \(y'=\frac{ax^2-2ax+b}{\left(x-1\right)^2}\) ta có y'(O)=b=-3 suy ra a=-2
vậy ta tìm đc a và b

Đáp án B
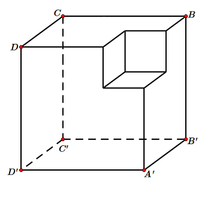
Gọi M là đỉnh của hình lập phương có cạnh bằng 1 nằm trên đường chéo AC’ và nằm trên khối còn lại sau khi cắt. Gọi I là tâm của khối cầu có thể tích lớn nhất thỏa mãn yêu cầu bài toán.
Ta có d I ; A ' B ' C ' D ' = d I ; B C C ' B ' = d I ; D C C ' D '
Suy ra I thuộc đoạn thẳng C’M và mặt cầu tâm I cần tìm đi qua điểm M.
Đặt d I ; D C C ' D ' = a , ta có IC' = a 3 mà A C ' = 3 3 , A M = 3
Suy ra I M = 2 3 - a 3 mặt khác d I ; D C C ' D ' = I M ⇔ a = 2 3 - a 3 ⇒ a = 3 - 3 3
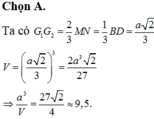


Đáp án là A
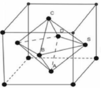
Cạnh của hình bát diện đều bằng:
a 2 2 ⇒ S d a y = a 2 2 2 = a 2 2
Thể tích cần tính: V = 2 3 h . S d a y = 2 3 a 2 a 2 2 = a 3 6