Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Thể tích của khối nón là V n = 1 3 π r 2 h 1 và độ dài đường sinh là l = r 2 + h 2
Thể tích của khối trụ là V t = π r 2 h 2 = 1 3 π r 2 h
Vậy thể tích cái nắp là V = V n + V t = 2 3 π r 2 h
Mặt khác l =1,25
⇒ r 2 + h 2 = 25 4 ⇔ r 2 = 25 4 − h 2
khi đó:
V = 2 3 π h 25 4 − h 2 ≤ 2 π 3 . 125 12 3
Ta có:
V 2 = 4 9 π 2 h 2 25 4 − h 2 2 ≤ 2 9 π 2 . 25 4 − h 2 . 25 4 − h 2 2 9 π 2 . 25 4 − h 2 . 25 4 − h 2 ≤ 2 π 2 9 . 25 4 + 25 4 3 3
Dấu bằng xảy ra khi:
2 h 2 = 25 4 − h 2 ⇔ h 2 = 25 12 ⇒ h = 5 2 3
Dấu “=” xảy ra khi:
2 h 2 = 25 4 − h 2 ⇔ h 2 = 25 12 ⇒ h = 5 2 3 ⇒ r = 25 4 − h 2 = 5 6 6 ⇒ r + h ≃ 348 c m

hoành độ giao điểm là nghiệm của pt
\(x^3-3mx^2+3\left(2m-1\right)x+1=2mx-4m+3\Leftrightarrow x^3-3mx^2+4mx-3x-2+4m=0\Leftrightarrow x^3-3x-2-m\left(3x^2-4x+4\right)=0\)
giải hệ pt ta có \(C_m\) luôn đi qua điểm A là nghiệm của hệ pt sau
\(\begin{cases}3x^2-4x+4=0\\x^3-3x-2=0\end{cases}\)
ta đc điều phải cm

Áp dụng định lí Pytago ta tính được
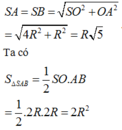
Nửa chu vi tam giác ABC là
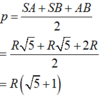
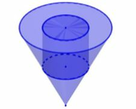
Do khối cầu nằm vừa khít trong hình nón nên bán kính cầu chính bằng bán kính đường tròn nội tiếp tam giác SAB.
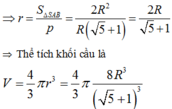
Thể tích khối cầu chính bằng thể tích phần nước dâng lên trong hình trụ có bán kính đáy R.
Gọi h là chiều cao cột nước dâng lên ta có
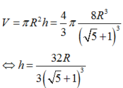
Chọn A.

Chọn mình nha
đáy bé dài:
129 . 3/4 = 104,25 (m)
Chiều cao dài:
104,25 : 5/8 = 166,8 (m)
Diện tích mảnh đất đó là:
(129 + 104,25). 166,8 : 2 = 19453,05 (m2)
= 194,4305 ha

\(\frac{x-4}{y-3}=\frac{4}{3}\Rightarrow\frac{x-4}{4}=\frac{y-3}{3}\)
Áp dụng TC của DTSBN ta có:
\(\frac{x-4}{4}=\frac{y-3}{3}=\frac{x-4-y+3}{4-3}=\frac{5-1}{1}=4\)
Suy ra: (x-4)/4=4 =>x-4=16=>x=20
(y-3)/3=4=>y-3=12=>x=15
x-4/y-3=4/3
=>3.(x-4)=4.(y-3)
=>3x-12=4y-12
=>3x=4y
Mà x-y=5=>x=y+5
=>3.(y+5)=4y
=>3y+15=4y=>4y-3y=15=>y=15
Khi đó x=15+5=20
Vậy x=20;y=15

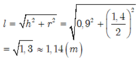




Đáp án A.
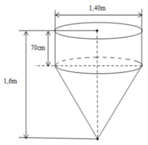
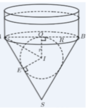
Diện tích cần tính gồm diện tích xung quanh hình trụ và diện tích xung quanh hình nón.