Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Hướng dẫn giải:
Thời gian để tụ phòng hết điện tích (q0 -> 0) được tính như sau
\(t = \frac{\varphi}{\omega}=\frac{\pi/2}{2\pi/T}=\frac{T}{4} \) => \(T = 4.2.10^{-6}= 8.10^{-6}s.\)
\(I_0 = q_0.\omega = 10^{-8}.\frac{2\pi}{8.10^{-6}}= 2,5.\pi.10^{-3} => I = \frac{I_0}{\sqrt{2}} \approx 5,55 mA.\)
khó không làm nổi
Ta có: \(\frac{1}{2}CU^2_{max}=\frac{1}{2}Li^2+\frac{1}{2}C^2_u\Rightarrow i=\sqrt{\frac{C}{L}\left(U^2_{max}-u^2\right)}\)\(=0,0447A=44,7mA\)
chọn D
\(\frac{1}{2}Li^2+\frac{1}{2}Cu^2=\frac{1}{2}CU_0^2\Rightarrow i=44,7mA\)
=> D đúng
mình bị nhầm ở đáp án
A. \(\frac{4}{3}\mu s\) các câu khác cũng như vậy nhé
Năng lượng của mạch dao động W = \(\frac{Q_0^2}{2C}=\frac{LI^2_0}{2}\) → chu kì dao động của mạch
\(T=2\pi\sqrt{LC}=2\pi\frac{Q_0}{I_0}=16.10^{-6}\left(s\right)=16\mu s\).Thời gian điện tích giảm từ Q0 dến Q0/2
q = Q0cos \(\frac{2\pi}{T}t=\frac{Q_0}{2}\rightarrow\frac{2\pi}{T}t=\frac{\pi}{3}\rightarrow t=\frac{T}{6}=\frac{8}{3}\mu s\)
→ C
\(C = \frac{1}{\omega^2.L}= 5.10^{-6}F.\)
\(U_0 = \frac{q_0}{C}= \frac{I_0}{C.\omega}= \frac{I_0.\sqrt{L}}{\sqrt{C}} = 8V.\)
\(i = I = \frac{I_0}{\sqrt{2}}. \)
\(\left(\frac{u}{U_0}\right)^2+\left(\frac{i}{I_0}\right)^2=1\)
=> \(\left(\frac{u}{U_0}\right)^2 = 1- \left(\frac{i}{I_0}\right)^2 = 1 - \frac{1}{2}= \frac{1}{2}\)
=> \(u = \frac{1}{\sqrt{2}}U_0= 4\sqrt{2}V.\)
Sử sụng hệ thức: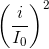 
+
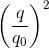= 1
Thay số và giải hệ phương trình trìm I0 và q0
Tần số góc: ω =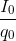 
= 50 (rad/s)
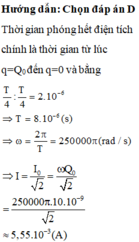
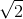
Chọn đáp án D
Thời gian phóng hết điện tích chính là thời gian từ lúc q = Q 0 đến q= 0 và bằng
T 4 : T 4 = 2.10 − 6 ⇒ T = 8.10 − 6 ( s ) ⇒ ω = 2 π T = 250000 π ( r a d / s )
⇒ I = I 0 2 = ω Q 0 2 = 250000 π .10.10 − 9 2 ≈ 5,55.10 − 3 ( A )