Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Khoảng thời gian giữa 2 lần liên tiếp động ăng bằng thế năng là T/4
\(\Rightarrow \dfrac{T}{4}=\dfrac{\pi}{40}\)
\(\Rightarrow T = \dfrac{\pi}{10}\)
\(\Rightarrow \omega=\dfrac{2\pi}{T}=20(rad/s)\)
Biên độ dao động: \(A=\dfrac{v_{max}}{\omega}=\dfrac{100}{20}=5(cm)\)
Ban đầu, vật qua VTCB theo chiều dương trục toạ độ \(\Rightarrow \varphi=-\dfrac{\pi}{2}\)
Vậy PT dao động là: \(x=5\cos(20.t-\dfrac{\pi}{2})(cm)\)

Khi lò xo chuyển động ra vị trí lò xo lớn nhất thì vận tốc của vật bằng 0
dao động mới sẽ có cùng biên độ với dao động cũ
Vận tốc cực đại sẽ là
\(v=A.\omega'=A\sqrt{\frac{k}{m_1+m_2}}=0,5m\text{/s }\)
\(\rightarrow D\)

Chọn trục toạ độ có gốc ở VTCB, chiều dương hướng sang phải.
Phương trình dao động tổng quát là: \(x=A\cos(\omega t+\varphi)\)
Theo thứ tự, ta lần lượt tìm \(\omega;A;\varphi\)
+ \(\omega=\sqrt{\dfrac{k}{m}}=20\sqrt 2(rad/s)\)
+ Biên độ A: \(A^2=x^2+\dfrac{v^2}{\omega^2}=3^2+\dfrac{(80\sqrt 2)^2}{(20\sqrt 2)^2}\)
\(\Rightarrow A = 5cm\)
+ Ban đầu ta có \(x_0=3cm\); \(v_0=-80\sqrt 2\) (cm/s) (do ta đẩy quả cầu về VTCB ngược chiều dương trục toạ độ)
\(\cos\varphi=\dfrac{x_0}{A}=\dfrac{3}{5}\); có \(v_0<0 \) nên \(\varphi > 0\)
\(\Rightarrow \varphi \approx0,3\pi(rad)\)
Vậy PT dao động: \(x=5\cos(20\sqrt 2+0,3\pi)(cm)\)

Hướng dẫn: Chọn đáp án A
Vì va chạm mềm nên tốc độ của hai vật ngay sau va chạm:
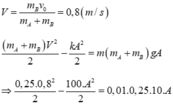
⇒ A = 0 , 03975 ( m )
![]()
![]()
![]()
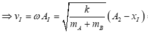
= 0,77 (m/s)
Chú ý: Giả sử lúc đầu vật ở vị trí biên, muốn tìm tốc độ hoặc tốc độ cực đại sau thời điểm t0 thì ta phân tích
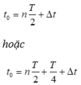
Từ đó tìm biên độ so với tâm dao động ở lần cuối đi qua O và tốc độ ở điểm cần tìm.

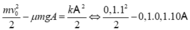



Va cham mềm nên động lượng của hệ 2 vật (M và m) bảo toàn: mv0 = (m+M) V.
Suy ra vận tốc của hệ 2 vật ngay lúc va chạm:
v = \(\upsilon=\frac{m\upsilon_0}{m+M}=\frac{0,01.10}{0,01+0,24}=\frac{0,1}{0,25}\) = 0,4 m/s = 40 cm/s
Hệ 2 vật dao động với tần số góc mới \(\omega=\sqrt{\frac{k}{m+M}}=\sqrt{\frac{16}{\left(0,01+0,24\right)}}\) = 8rad/s
Vì hệ nằm ngang nên biên độ dao động được tính theo công thức
\(A^2=x^2=\frac{v^2}{\omega^2}=0^2+\frac{v^2}{\omega^2}=\frac{40^2}{16}=100\)
Vậy biên độ dao động: A = 10cm
→ B