Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Ta có : tại thời điểm x = -10 cm vật ở vị trí trên đường tròn số 2 hoặc số 3
Giả sử ta chọn nó đang ở vị trí trên đường tròn số 2 , xét tiếp sau đó khoảng thời gian 3 T 4 ở vị trí đường tròn số 1.
Mà vận tốc v nhanh pha hơn li độ x một góc là π 2
x 1 v à v và v cùng pha ta có : - 10 A = - 100 ω A ⇒ ω = 10 r a d / s

Ta có :
\(A=l'=\frac{mg}{k}=\frac{g}{\omega^2}\)
\(v_0=A\omega\Rightarrow\frac{g}{\omega}=v_0\Rightarrow\omega=\frac{g}{v_0}\)
\(\Rightarrow A=\frac{g}{\omega^2}=\frac{v^2_0}{g}=6,25\left(cm\right)\)

Khoảng thời gian giữa 2 lần liên tiếp động ăng bằng thế năng là T/4
\(\Rightarrow \dfrac{T}{4}=\dfrac{\pi}{40}\)
\(\Rightarrow T = \dfrac{\pi}{10}\)
\(\Rightarrow \omega=\dfrac{2\pi}{T}=20(rad/s)\)
Biên độ dao động: \(A=\dfrac{v_{max}}{\omega}=\dfrac{100}{20}=5(cm)\)
Ban đầu, vật qua VTCB theo chiều dương trục toạ độ \(\Rightarrow \varphi=-\dfrac{\pi}{2}\)
Vậy PT dao động là: \(x=5\cos(20.t-\dfrac{\pi}{2})(cm)\)

Đáp án A
Phương pháp: Sử dụng đường tròn lượng giác và lí thuyết về con lắc lò xo treo thẳng đứng
Cách giải:
- Độ dãn của lò xo khi vật ở vị trí cân bằng:
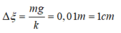
- Kéo vật xuống khỏi vị trí cân bằng theo phương thẳng đứng 2 cm rồi buông nhẹ nên biên độ dao động của vật: A = 2cm.
- Chu kỳ dao động T = 0,2s.
- Lò xo bị nén khi vật di chuyển trong đoạn từ li độ -1cm và biên âm -2cm, được biểu diễn bằng phần tô đậm như hình vẽ.
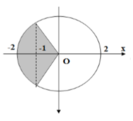
- Trong 0,5s = 2,5T, thời gian lò xo bị nén là: 2T/3 + T/6 = 1,6 (s)

Ban đầu \(v_0=0\) (cm/s)
Tốc độ của vật tăng thêm \(30\pi\) (cm/s) \(\Rightarrow v_1=30\pi\) (cm/s)
Vì vận tốc là đại lượng biến thiên điều hòa theo thời gian nên ta có thể biểu diễn nó bằng véc tơ quay.
Trong thời gian T/12, góc quay là: \(\alpha=360/12=30^0\)
Ta có:
> v M N O 30π 30°
Ban đầu véc tơ quay ở M ứng với v = 0, lúc sau véc tơ quay đến N.
Ta có: \(30\pi=v_{max}.\sin 30^0\)
\(\Rightarrow v_{max}=60\pi(cm/s)\)
\(\Rightarrow \omega=\dfrac{v_{max}}{A}=5\pi(rad/s)\)
Chu kì: \(T=2\pi/\omega=0,4s\)

Chọn đáp án A
? Lời giải:

+ Lực đàn hồi đổi chiều tại vị trí lò xo không biến dạng.
+ Lực hồi phục (kéo về) đổi chiều tại vị trí cân bằng

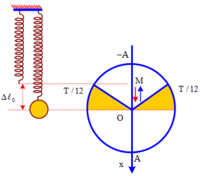
+ Thời gian mà lực đàn hồi ngược chiều lực hồi phục khi vật đi từ O đến M (M là vị trí lò xo không biến dạng) và ngược lại
![]()

Chọn đáp án A
? Lời giải:
+ Lực đàn hồi đổi chiều tại vị trí lò xo không biến dạng.
+ Lực hồi phục (kéo về) đổi chiều tại vị trí cân bằng
f = 1 2 π g Δ l ⇒ Δ l = 1 c m A = Δ l 2 + v 2 ω 2 = 2 c m ⇒ Δ l = A 2
+ Thời gian mà lực đàn hồi ngược chiều lực hồi phục khi vật đi từ O đến M (M là vị trí lò xo không biến dạng) và ngược lại
Δ t = 2. T 12 = T 6 = 1 30 s

\(A=l'=\frac{mg}{k}=\frac{g}{\omega^2}\)
\(v_0=A\omega\Rightarrow\frac{g}{\omega}=v_0\Rightarrow\omega=\frac{g}{v_0}\)
\(\Rightarrow A=\frac{g}{\omega^2}=\frac{v^2_0}{g}=6,25\left(cm\right)\)
Đáp án C
+ Trước khi buông, lực giữ vật chính bằng lực kéo về max => F k m ax = k A = m ω 2 A = 2 ( N ) (1)
+ 2 thời điểm gốc thời gian và ∆ t = 3 T / 4 vuông pha nhau nên ta có
v 2 = ω x 1 v 1 = − ω x 2 ⇒ − 1 = ω . ( − 0 , 1 ) ⇒ ω = 10 ( r a d / s ) . Thay vào (1) tìm được A = 20 (cm)
+ Có v 2 = − 1 ( m / s ) = − v m ax 2 và đang tăng ⇒ ϕ v 2 = − 2 π 3 ⇒ ϕ x 2 = 5 π 6 ⇒ ϕ x 1 = φ = − 2 π 3