

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án D
+ Trọng lực của quả cầu: P = mg = 01.10 = 1 N
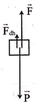
+ Ta có: P > F nên muốn quả cầu nằm cân bằng thì khi đó phải có chiều hướng lên và có độ lớn thỏa mãn:
F d h + F = P ⇒ F d h = P - F = 1 - 0.8 = 0,2 N
+ Độ giãn của lò xo tại vị trí bắt đầu thả vật: ∆ l = F d h k = 0 , 2 40 = 0 . 005 ( m ) = 0 , 5 ( c m )
+ Độ giãn của lò xo tại VTCB: ∆ l 0 = m g k = 1 40 = 0 . 025 ( m ) = 2 , 5 c m
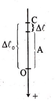
+ Từ hình bên ta có: A = = ∆ l 0 - ∆ l = 0 , 025 - 0 , 005 = 0 , 02 m
+ Lực đàn hồi cực đại tác dụng lên giá treo:
F d h m a x = k ( ∆ l 0 + A ) = 40 ( 0 , 025 + 0 , 02 ) = 1 , 8 N
+ Do ∆ l 0 > A nên lực đàn hồi cực tiểu:
F d h m i n = k ( ∆ l 0 - A ) = 40 ( 0 , 025 - 0 , 02 ) = 0 , 2 N

Độ biến dạng của lò xo khi vật ở VTCB là: \(\Delta \ell_0=\dfrac{mg}{k}=\dfrac{1.10}{100}=0,1m=10cm\)
\(\omega=\sqrt{\dfrac{k}{m}}=10(rad/s)\)
Áp dụng CT: \(A^2=x^2+\dfrac{v^2}{\omega^2}\)
\(\Rightarrow A^2=2^2+\dfrac{(20\sqrt 3)^2}{10^2}\)
\(\Rightarrow A = 4cm\)
Lực đàn hồi cực đại:
\(F_{dhmax}=k\Delta\ell_{max}=k(\Delta\ell_0+A)=100.(0,1+0,04)=14(N)\)
Lực đàn hồi cực tiểu:
\(F_{dhmin}=k\Delta\ell_{min}=k(\Delta\ell_0-A)=100.(0,1-0,04)=6(N)\)

Gọi biên độ dao động là A.
Độ dãn của lò xo khi vật ở VTCB là: \(\Delta\ell_0=\dfrac{mg}{k}\)
Độ dãn cực đại của lò xo là: \(\Delta\ell_0+A=10cm=0,1m\)
Lực đàn hồi cực tiểu là: \(k(\Delta\ell_0-A)=0,8\)
\(\Rightarrow k(\Delta \ell_0+\Delta\ell_0-0,1)=0,8\)
\(\Rightarrow k(2\Delta \ell_0-0,1)=0,8\)
\(\Rightarrow k(2\dfrac{mg}{k}-0,1)=0,8\)
\(\Rightarrow2.mg-0,1.k=0,8\)
\(\Rightarrow2.0,24.10-0,1.k=0,8\)
\(\Rightarrow k=40(N/m)\)
Lực mà lò xo tác dụng lên vật khi lò xo dãn 5cm là lực đàn hồi của lò xo và bằng: \(F=k.\Delta\ell=40.0,05=2(N)\)

Kéo vật từ vị trí cân bằng xuống dưới 3cm thì thả vật ra => \(A = 3cm.\)
Hòn bi thực hiện 50 dao động toàn phần trong 20 s
=> Thời gian thực hiện 1 dao động toàn phần (chính là chu kỳ T) : \(T = \frac{20}{50} = 0,4 s.\)
\(\Delta l\) là độ dãn của lò xo khi ở vị trí cân bằng. Tại vị trí cân bằng: \(P = F_{đh}\)
=> \(mg = k\Delta l=> T = 2\pi \sqrt{\frac{m}{k}} = 2\pi\sqrt{\frac{\Delta l}{g}}.\)
=> \(\Delta l = \frac{T^2.g}{4\pi^2} = \frac{T^2}{4} = 0,04 m = 4cm.\)
Lực đàn hồi cực tiểu khác 0 => \(\Delta l \geq A\) => Lực đàn hồi cực tiểu là \(F_{đhmin}=k(\Delta l -A).\)
=> \(\frac{F_{đhmax}}{F_{đhmin}} = \frac{k(\Delta l +A)}{k(\Delta l -A)} = \frac{\Delta l +A}{\Delta l -A} = \frac{4+3}{4-3}= 7.\)

Đáp án A
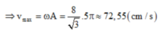
∆ l 01 = m g k = 2 c m
ω = k m = 10 5 rad/s
∆ l 02 = m ' g k = 2 , 5 c m
Tại VTCB sau đó , lò xo giản 2,5 cm , tại thời điểm quả cầu tới biên dưới O lò xo giản 6 cm
=> A' = (6-2,5) = 3,5 cm; ω 2 = k m ' = 20
Vị trí O ban đầu cách VTCB lúc sau 0,5 cm
![]()
![]()