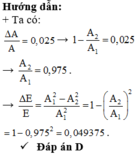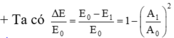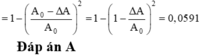Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án D.
Năng lượng trong một dao động toàn phần (một chu kì):
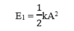
Sau mỗi chu kì biên độ giảm 3%.
Năng lượng toàn phần sau mỗi chu kì:
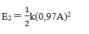
=> Năng lượng bị mất trong một dao động toàn phần:
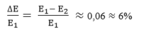

Đáp án A
Ta có:
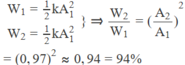
Phần cơ năng của con lắc bị mất đi trong một chu kì là 6%

Đáp án A
Giả sử biên độ ban đầu của con lắc là A0. Sau một chu kỳ biên độ con lắc giảm 3% nên biên độ còn 0,97A0. Năng lượng của con lắc sau một chu kỳ dao động là W = 1 2 k A ' 2 = 1 2 k ( 0 , 97 A ) 2 = 0 , 94 W 0
Phần năng lượng của con lắc bị mất đi trong một dao động toàn phần là
W 0 - W = W 0 - 0.94 W 0 = 0,06 W 0 = 6% W 0

Gia tốc biểu kiến của con lắc nằm trong thang máy chuyển động với gia tốc \(\overrightarrow a\) là:
\(\overrightarrow {g'} = \overrightarrow {g} -\overrightarrow a \)
Thang máy đi lên chậm dần đều nên \(\overrightarrow g \uparrow \uparrow \overrightarrow a\) => \( {g'} ={g} -a \)
Mà \(a = \frac{g}{2} => g' = g - \frac{g}{2} = \frac{g}{2}.\)
Chu kì của con lắc lúc này là \(T' =2\pi \sqrt{\frac{l}{g}} = 2\pi \sqrt{\frac{2l}{g}} = T\sqrt{2}.\)

Khoảng thời gian vận tốc của vật không vượt quá \(6\pi cm/s\) là \(\frac{\Delta t}{T}=\frac{1}{3}\)
\(\Rightarrow\)Góc quét: \(\Delta\varphi=\frac{2\pi}{T}\frac{T}{3}=\frac{2\pi}{3}\left(rad\right)\)
\(\Rightarrow\) VTLG
-v
\(\Rightarrow\cos\varphi=\cos\left(90-30\right)=\frac{v}{v_{max}}=\frac{1}{2}\Rightarrow v_{max}=12\pi=\)\(\omega A\Rightarrow A=3,6cm\)