
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(2M=\frac{3-1}{1.2.3}+\frac{4-2}{2.3.4}+\frac{5-3}{3.4.5}+...+\frac{12-10}{10.11.12}=\)
\(=\frac{1}{1.2}-\frac{1}{2.3}+\frac{1}{2.3}-\frac{1}{3.4}+\frac{1}{3.4}-\frac{1}{4.5}+...+\frac{1}{10.11}-\frac{1}{11.12}=\frac{1}{2}-\frac{1}{11.12}\)
\(\Rightarrow M=\frac{1}{4}-\frac{1}{11.24}=\frac{66-1}{11.24}=\frac{65}{11.24}\)



Số ngày trong một tuần lễ là 7 ngày thì gấp đôi số ngày trong một tuần lễ là 14.
Suy ra = 14.
Gấp đôi là 14.2 = 28.
Vì gấp đôi của nên = 28.
Vậy năm đó là năm 1428.
Bạn ht

Vì khi học sinh lớp 6C xếp hàng 2, hàng 3, hàng 4, hàng 8 đều đủ hàng có nghĩa là số học sinh ấy là bội chung của 2, 3, 4, 8.
BCNN(2, 3, 4, 8) = 24. Mỗi bội của 24 cũng là một bội chung của 2, 3, 4, 8. Vì số học sinh của lớp 6C trong khoảng 35 đến 60 nên ta phải chọn bội của 24 thỏa mãn điều kiện này. Đó là 24 . 2 = 48.
Vậy lớp 6C có 48 học sinh.
Gọi số học sinh của lớp 6C là a
Vì a xếp hàng 2,hàng 3,hàng 4,hàng 8 đều vừa đủ hàng
nên:
a ϵ BC(2,3,4,8) và 35<a<60
Ta có: BCNN(2,3,4,8) = 24
Mà a ϵ BC(2,3,4,8) và 35<a<60 nên ta có:
+) a = 24 . 2 = 48 (nhận)
+) a = 24 . 3 = 72 (loại)
+) a = 24 . 4 = 96 (loại)
+ a) = 24 . 8 = 192 (loại)
\(\Rightarrow\) chỉ có 1 gia trị a thỏa mãn đề bài là a = 48
Vậy số học sinh lớp 6C là 48 học sinh

a)
- Vì 84 và 180 cùng chia hết cho x nên x là ƯC(84, 180). - Tìm ƯC(84, 180) thông qua tìm ƯCLN(84, 180) + Phân tích: 84 = 22.3.7 180 = 22.32.5 + Các thừa số chung là 2, và 3 + Số mũ nhỏ nhất của 2 là 2, của 3 là 1. Do đó ƯCLN(84, 180) = 22.3 = 12 Suy ra ƯC(84, 180) = {1, 2, 3, 4, 6, 12} - Vì x > 6 nên x = 12
Vậy A = {12}
b)
- Vì x chia hết cho cả 12, 15 và 18 nên x là BC(12, 15, 18). - Tìm BC(12, 15, 18) thông qua tìm BCNN(12, 15, 18) + Phân tích: 12 = 22.3 15 = 3.5 18 = 2.32 + Chọn thừa số chung, riêng: đó là 2, 3, 5 + Số mũ lớn nhất của 2 và 3 là 2, của 5 là 1. Do đó BCNN(12, 15, 18) = 22.32.5 = 180 Suy ra BC(12, 15, 18) = {0, 180, 360, 540, ...} - Vì 0 < x < 300 nên x = 180
Vậy B = {180}
a)
- Vì 84 và 180 cùng chia hết cho x nên x là ƯC(84, 180). - Tìm ƯC(84, 180) thông qua tìm ƯCLN(84, 180) + Phân tích: 84 = 22.3.7 180 = 22.32.5 + Các thừa số chung là 2, và 3 + Số mũ nhỏ nhất của 2 là 2, của 3 là 1. Do đó ƯCLN(84, 180) = 22.3 = 12 Suy ra ƯC(84, 180) = {1, 2, 3, 4, 6, 12} - Vì x > 6 nên x = 12
Vậy A = {12}
b)
- Vì x chia hết cho cả 12, 15 và 18 nên x là BC(12, 15, 18). - Tìm BC(12, 15, 18) thông qua tìm BCNN(12, 15, 18) + Phân tích: 12 = 22.3 15 = 3.5 18 = 2.32 + Chọn thừa số chung, riêng: đó là 2, 3, 5 + Số mũ lớn nhất của 2 và 3 là 2, của 5 là 1. Do đó BCNN(12, 15, 18) = 22.32.5 = 180 Suy ra BC(12, 15, 18) = {0, 180, 360, 540, ...} - Vì 0 < x < 300 nên x = 180
Vậy B = {180}

Câu 6.1 trang 16 Sách Bài Tập (SBT) Toán lớp 6 tập 2
Trong các phân số sau, phân số lớn hơn 3535 là
(A)1120;(A)1120;
(B)815;(B)815;
(C)2235;(C)2235;
(D)2340.(D)2340.
Hãy chọn đáp số đúng
Giải
Chọn đáp án (C)2235;(C)2235;
Câu 6.2 trang 16 Sách Bài Tập (SBT) Toán lớp 6 tập 2
Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai?
a) Không có phân số nào lớn hơn 3737 và nhỏ hơn 4747
b) Nếu một phân số có tử lớn hơn mẫu thì phân số đó lớn hơn 1.
Giải
a) Sai, ví dụ 37<12<4737<12<47
b) Sai, ví dụ −2−3<−1−2−3<−1. Khẳng định ở câu b) đúng nếu tử và mẫu đều dương.
Câu 6.3 trang 16 Sách Bài Tập (SBT) Toán lớp 6 tập 2
Tìm hai phân số có mẫu khác nhau, các phân số này lớn hơn 1515 nhưng nhỏ hơn 1414
Giải
Chọn mẫu chung là 60 ta có: 15=1260,14=156015=1260,14=1560
Ta có 1260<1360<1460<15601260<1360<1460<1560
Rút gọn các phân số này ta được: 15<1360<730<1415<1360<730<14
Ta tìm được hai phân số 13601360 và 730730 có mẫu khác nhau, lớn hơn 1515 nhưng nhỏ hơn 1414.
Câu 6.4 trang 16 Sách Bài Tập (SBT) Toán lớp 6 tập 2
a) Chứng tỏ rằng trong hai phân số cùng tử, tử và mẫu đều dương, phân số nào có mẫu nhỏ hơn thì lớn hơn.
Nếu a, b, c > 0 và b < c thì ab>acab>ac
b) Áp dụng tính chất trên, hãy so sánh các phân số sau:
937937 và 12491249; 3023530235 và 16813231681323; 321454321454 và 325451325451
Giải
a) ab=acbc,ac=abbcab=acbc,ac=abbc
Vì c > b nên ac > ab. Suy ra acbc>abacacbc>abac. Vậy ab>acab>ac
b) 937=36148,1249=36147937=36148,1249=36147. Ta có 36148<3614736148<36147 nên 947<1249947<1249
30235=647=24188;1681323=2418930235=647=24188;1681323=24189
Vì 24188>2418924188>24189 nên 30235>168132330235>1681323
321454<325454<325451⇒321454<325451321454<325454<325451⇒321454<325451



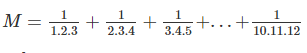
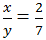
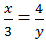

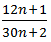 là phân số tối giản (n ∈ N)
là phân số tối giản (n ∈ N)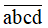
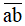 gấp đôi số ngày trong một tuần lễ, còn
gấp đôi số ngày trong một tuần lễ, còn 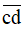 gấp đôi của
gấp đôi của 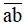 . Tính xem năm đó là năm nào.
. Tính xem năm đó là năm nào.
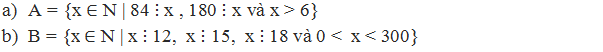
 giải hộ mk với
giải hộ mk với 
Cách vẽ: vẽ 2 đường chéo của hình vuông ta được 4 hình tam giác bằng nhau, tô màu một hình tam giác ta được 1/4 của hình vuông (hình 1).