Điền phân số thích hợp vào ô vuông:

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mua vip

Pham Trong Bach

14 tháng 9 2019

Điền phân số thích hợp vào ô vuông: - 8 13 - □ = 0 .

#Toán lớp 6

Cao Minh Tâm

14 tháng 9 2019

Đúng(0)

Các câu hỏi dưới đây có thể giống với câu hỏi trên

Pham Trong Bach

25 tháng 4 2018

Điền phân số thích hợp vào ô vuông: - 1 3 + □ = 2 5 .

#Toán lớp 6

Cao Minh Tâm

25 tháng 4 2018

Đúng(0)

Sách Giáo Khoa

17 tháng 4 2017

Điền phân số thích hợp vào ô trống :

a) \(\dfrac{1}{12}+.....=\dfrac{-2}{3}\)

b) \(\dfrac{-1}{3}+......=\dfrac{2}{5}\)

c) \(\dfrac{1}{4}-......=\dfrac{1}{20}\)

d) \(\dfrac{-8}{13}-......=0\)

#Toán lớp 6

Lưu Hạ Vy

17 tháng 4 2017

Coi phân số phải tìm là x rồi vận dụng quy tắc chuyển vế để tìm x.

Chẳng hạn:

\(c)\) \(\dfrac{1}{4}-x=\dfrac{1}{20}\) . Chuyển vế thì ta đc :

\(x=\dfrac{1}{5}\)

Đáp số:

\(a)-\dfrac{3}{4}\)

b) \(\dfrac{11}{15}\)

c) \(\dfrac{1}{5}\)

d) \(-\dfrac{8}{13}\)

Đúng(0)

Sách Giáo Khoa

15 tháng 5 2017

Điền phân số thích hợp vào ô vuông :

a) \(\dfrac{3}{7}+....=\dfrac{-2}{7}\)

b) \(......+\dfrac{-5}{11}=\dfrac{-13}{11}\)

c) \(\dfrac{6}{18}+\dfrac{3}{18}=.....\)

d) \(\dfrac{-6}{17}+.....=\dfrac{-6}{17}\)

#Toán lớp 6

hồ quỳnh anh

16 tháng 5 2017

a)-5/7

b)-8/11

c)9/18 = 1/2

d)0

Đúng(0)

Hải Đăng

3 tháng 5 2018

Giáº£i sÃ¡ch bÃ i táºp ToÃ¡n 6 | Giáº£i bÃ i táºp SÃ¡ch bÃ i táºp ToÃ¡n 6

Đúng(0)

Sách Giáo Khoa

15 tháng 5 2017

Điền số thích hợp vào ô vuông :

\(\dfrac{-8}{15}< \dfrac{.....}{40}< \dfrac{-7}{15}\)

#Toán lớp 6

MonKey D. Luffy

12 tháng 8 2017

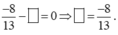
Ta có :

MSC của 15 và 40 là 120

Suy ra -8/15 = -64/120

-7/15 = -56/120

Gọi số cần tìm là x ta có

-64/120 < 3x/120 < -56/120

Vậy 3x có thể là -62 ; -60 ; -58

Đúng(0)

Trang Thùy

17 tháng 9 2018

Ta có \(\dfrac{-8}{15}< \dfrac{...}{40}< \dfrac{-7}{15}\)

=> \(\dfrac{-64}{120}< \dfrac{3...}{120}< \dfrac{-56}{120}\)

=> Vậy số nguyên cần điền vào ô trống là -20; -21; -19

Đúng(0)

Pham Trong Bach

22 tháng 7 2018

Điền số thích hợp vào ô vuông:

□ 8 = - 28 32

#Toán lớp 6

Cao Minh Tâm

22 tháng 7 2018

Đúng(0)

Pham Trong Bach

2 tháng 5 2017

Điền số thích hợp vào ô vuông:

□ 8 = - 28 32

#Toán lớp 6

Cao Minh Tâm

2 tháng 5 2017

Đúng(0)

Pham Trong Bach

16 tháng 10 2019

Điền phân số thích hợp vào ô vuông: 1 12 + □ = - 2 3 .

#Toán lớp 6

Cao Minh Tâm

16 tháng 10 2019

Đúng(0)

Pham Trong Bach

16 tháng 6 2019

Điền phân số thích hợp vào ô vuông: 1 4 - □ = 1 20 .

#Toán lớp 6

Cao Minh Tâm

16 tháng 6 2019

Đúng(0)

Mình yêu các bạn trên Hoc24.vn nhiề...

27 tháng 9 2016

Cho phân số \(\frac{a}{b}>1\), m là một số tự nhiên \(\ne\) 0. Hãy điền dấu ( >, <, = ) thích hợp vào ô trống:

\(\frac{a}{b}.....\frac{a+m}{b+m}\)

#Toán lớp 6

Trần Thị Bảo Trân

27 tháng 9 2016

Ta có:

\(\frac{a}{b}=\frac{a\times\left(b+m\right)}{b\times\left(b+m\right)}=\frac{a\times b+a\times m}{b\times b+b\times m}\)

\(\frac{a+m}{b+m}=\frac{\left(a+m\right)\times b}{\left(b+m\right)\times b}=\frac{a\times b+m\times b}{b\times b+b\times m}\)

vì \(\frac{a}{b}>1\) nên \(a>b\), ta suy ra \(a\times m>b\times m\)

hay \(a\times b+a\times m>a\times b+m\times b\)

hay \(\frac{a\times b+a\times m}{b\times b+b\times m}>\frac{a\times b+m\times b}{b\times b+b\times m}\)

hay \(\frac{a}{b}>\frac{a+m}{b+m}\)

Đúng(0)

soyeon_Tiểubàng giải

27 tháng 9 2016

Vì \(\frac{a}{b}>1\)

=> a > b

=> a.m > b.m

=> a.m + a.b > b.m + a.b

=> a.(b + m) > b.(a + m)

=> \(\frac{a}{b}>\frac{a+m}{b+m}\)

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP