Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

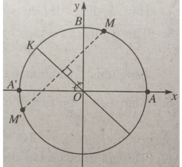
Sđ MK = sđ KM’ = 55 o
⇒ sđ AM’ = sđ AM + sđ MK + sđ KM’ = 190 o .
Đáp án: C

Cách 1. Suy luận.
Điểm M nằm ở góc phần tư thứ IV nên điểm M 1 nằm ở góc phần tư thứ hai. Số đo A M 1 dương nên hai phương án A, D bị loại. Mặt khác sđ A M 1 < 180 o nên phương án B bị loại.
Vậy đáp án là C.
Cách 2. Tính trực tiếp.
Gọi B là giao điểm của đường phân giác góc xOy với đường tròn. Ta có
Sđ A B = 45 o , s đ M A = 70 o
Suy ra sđ MB = 115 o .
Mà sđ B M 1 = sđ MB nên sđ A M 1 = 45 o + 115 o = 160 o .
Đáp án: C

Bài 1:
\(\Leftrightarrow-cosa-cosa+sina+cosa=0\Leftrightarrow sina=cosa\)
\(\Rightarrow a=\frac{\pi}{4}+k\pi\Rightarrow a\) thuộc cung thứ nhất và thứ 3
Bài 2:
Ta có \(\frac{5\pi}{3}-\left(-\frac{\pi}{3}\right)=\frac{6\pi}{3}=2\pi\Rightarrow\) góc \(\frac{5\pi}{3}\) và \(-\frac{\pi}{3}\) cùng cung biểu diễn

\(sinx+cosx=m\Rightarrow\left(sinx+cosx\right)^2=m^2\)
\(\Rightarrow1+2sinx.cosx=m^2\Rightarrow sinx.cosx=\frac{m^2-1}{2}\)
Ta co:
\(tan^2x+cot^2x=tan^2x+2tanx.cotx+cot^2x-2\)
\(=\left(tanx+cotx\right)^2-2=\left(\frac{sinx}{cosx}+\frac{cosx}{sinx}\right)^2-2=\left(\frac{sin^2x+cos^2x}{sinx.cosx}\right)^2-2\)
\(=\frac{1}{\left(sinx.cosx\right)^2}-2=\frac{1}{\left(\frac{m^2-1}{2}\right)^2}-2=\frac{4}{m^4-2m^2+1}-2\)
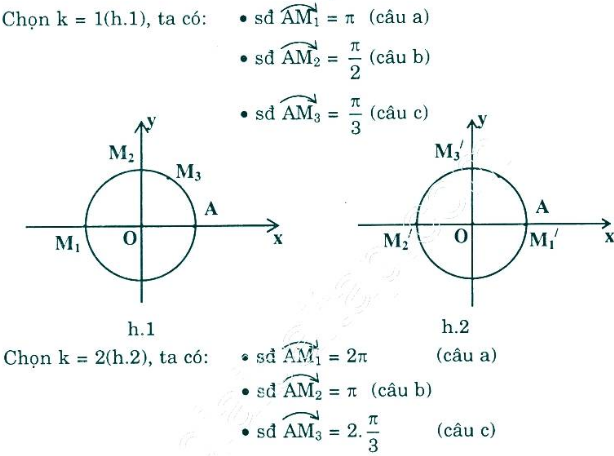
Chọn A.
Theo giả thiết ta có: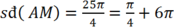
suy ra điểm M là điểm chính giữa của cung phần tư thứ I.