Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A.
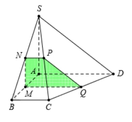
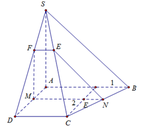
Gọi N, Q lần lượt là trung điểm của AB, CD ⇒ M N ⊥ A B M Q ⊥ A B .
Qua N kẻ đường thẳng song song với BC, cắt SC tại P.
Suy ra thiết diện của mặt phẳng α và hình chóp là MNPQ.
Vì MQ là đường trung bình của hình tháng ABCD ⇒ M Q = 3 a 2 .
MN là đường trung bình của tam giác SAB ⇒ M N = S A 2 = a .
NP là đường trung bình của tam giác SBC ⇒ N P = B C 2 = a 2 .
Vậy diện tích hình thang MNPQ là S M N P Q = M N . N P + M Q 2 = a 2 a 2 + 3 a 2 = a 2 .

a﴿ Chu vi:
2/5 x 4 = 8/5 ﴾m﴿
Diện tích:
2/5 x 2/5 = 4/25 ﴾m2 ﴿
b﴿ Diện tích 1 ô vuông nhỏ là:
2/25 x 2/25 = 4/625 ﴾m2 ﴿
Số ô vuông cắt được là:
4/25 : 4/625 = 25 ﴾ô vuông﴿
c﴿ Chiều rộng tờ giấy hình chữ nhật là:
4/25 : 4/5 = 1/5 ﴾m﴿




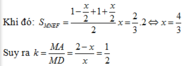
Đáp án A