Cho tam giác ABC vuông tại A, có AB = 1/3BC. Hãy tính sinC, cosC, tgC, cotgC.

K

Khách

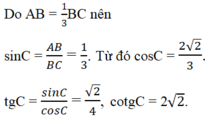
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mua vip

PT

Pham Trong Bach

21 tháng 6 2019

Cho tam giác ABC vuông tại A, có AB = 1/3BC. Hãy tính sinC, cosC, tgC, cotgC.

1

CM

Cao Minh Tâm

21 tháng 6 2019

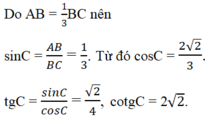
Giải sách bài tập Toán 9 | Giải bài tập Sách bài tập Toán 9

Các câu hỏi dưới đây có thể giống với câu hỏi trên

SG

Sách Giáo Khoa

27 tháng 4 2017

Cho tam giác ABC vuông tại A, có \(AB=\dfrac{1}{3}BC\). Hãy tính \(\sin C,\cos C,tgC,cotgC\) ?

1

NT

Nguyen Thuy Hoa

1 tháng 6 2017

Hệ thức lượng trong tam giác vuông

NT

Nguyễn Tuyết Minh

8 tháng 7 2016 - olm

Tính sinC, cosC, CotgC nếu biết tgC = 0.75. Giúp mình với :)

2

SS

Sakura Scarlet

8 tháng 7 2016

sinC=4/5

cosC= 3/5

CotgC= 3/4

NT

Nguyễn Tuyết Minh

9 tháng 7 2016

Bạn có thể ghi lời giải cho mình được không vậy?

LD

Lê Dương

16 tháng 7 2020 - olm

1.Vẽ tam giác ABC vuông tại A đường cao AH, tính BC,AH,CH,cosB,cosC,sinB,sinC theo trg hợp sau

1,AB=2cm, góc C =45 độ

2,AB=6cm,góc B= 60 độ

2. đề như b1 bỏ cos,sin tính tgB,tgC,cotgB,cotgC

1,AC=4cm,C=45 độ

2,AB=6,C=30 độ

3.đề như b1: 1,CH=75cm,C=30 độ 2, BH=2cm,B =45 độ làm giúp mình với 7h mình phải đi rồi :(((( cảm ơn ạ

2

LD

Lê Dương

16 tháng 7 2020

mng ơi giúp mình với ạ

PN

Phan Nghĩa

17 tháng 7 2020

mình trả lời hơi muộn :(

A B C H

1, Theo giả thiết ta có C = 45* nên tam giác ABC là tam giác vuông cân

Suy ra AB = AC = 2 (cm) Mà theo đánh giá của Pitago thì :BC^2 = 8 <=> BC = căn 8

Ta có hệ thức lượng sau : AB.AC=AH.BC <=> 4=căn 8 . AH<=> AH=2/căn2

Lại có hệ thức lượng sau : AC^2=CH.BC<=>4=căn 8 . CH <=> CH=2/căn2

Mặt khác : +)Cos alpha = AB/BC = 2/căn8 = 1/căn2

+)Cos beta = AC/BC = 2/căn8 = 1/căn2

+) Sin alpha = AC/BC = 2/căn8 = 1/căn2

+) Sin beta = AB/BC = 2/căn8 = 1/căn2

Vậy ...

Mấy câu còn lại để từ từ mình làm dần

BD

Bảo Duy

1 tháng 10 2023

a)Cho tam giác ABC vuông tại A, biết AB=4cm; BC=5cm, Tonhs cosC+TanB

b) Cho tam giác ABC vuông tại A, có AB=5cm,BC=10cm. Tính sinC và số đo góc B

c) Cho tam giác ABC vuông tại A, biết cosB=8cm. hãy tính các tỉ số lượng giác của góc C. E c.ơn ạ!

3

CH

Cee Hee

1 tháng 10 2023

Câu a) với b) tính cos, tan, sin là tính góc hay cạnh vậy cậu?

BD

Bảo Duy

1 tháng 10 2023

KK

Kim Kai

6 tháng 7 2018 - olm

Tính sinC, cosC, cotgC nếu biết tgC=0.75

Các bạn ghi cách giải giúp mình nha.

1

CV

cao van duc

6 tháng 7 2018

dung tinh chat : tanC.cotC=1=>cotC=4/3

sau đó dùng tính chất:\(1+cot^2C=\frac{1}{sin^2C}\Rightarrow sin^2C\)=0,36 =>sinC=0,6=>cosC=sinC / tanC=0,8

SG

son goku

9 tháng 8 2019 - olm

Cho tam giác ABC vuông tại A, cosC = 1/3.Tính sinB, sinC

1

TT

Thanh Tùng DZ

9 tháng 8 2019

Ta có : \(\widehat{B}+\widehat{C}=90^o\)

\(\Rightarrow\cos C=\sin B=\frac{1}{3}\)

Ta có : \(\sin^2C+\cos^2C=1\Rightarrow\sin^2C=1-\cos^2C=\frac{8}{9}\)

\(\Rightarrow\sin C=\frac{2\sqrt{2}}{9}\)

NK

Nguyễn Kim Giang

15 tháng 10 2015 - olm

cho tam giác ABC vuông tại A. Biết tanC= 0.75. Không tính số đo góc, tính cotC, sinC, cosC

1

NT

nguyen thi thu Thuy

15 tháng 10 2015

cotC=1/tanC = 4/3

=>\(\frac{ac}{ab}=\frac{4}{3}\)=>ac=4k , ab=3k {với k \(\ge\) 0 }

=>BC = 5k

=>sinC =\(\frac{3}{5}\)

cosC=\(\frac{4}{5}\)

tick nha

GB

Gia Bảo

10 tháng 8 2021

Cho tam giác ABC vuông tại A Biết :

1. sinc=1/3 tính AC. 2. cosc=2/5 tính AC

mong mn giúp đỡ

0

PH

Phạm Hà Nguyệt Anh

23 tháng 8 2021 - olm

Cho tam giác ABC vuông tại A, AC = 28cm, Tính độ dài các đoạn thẳng AB, BC biết:
a) cotC = \(\frac{7}{11}\)
b) tanC = \(\frac{5}{7}\)
c) cosC = \(\frac{4}{5}\)
d) sinC = \(\frac{3}{5}\)

1

NH

Nguyễn Huy Tú

23 tháng 8 2021

a, Xét tam giác ABC vuông tại A, đường cao AH

cotC = 7/11 => \(\frac{AB}{AC}=\frac{7}{11}\Rightarrow AB=\frac{7}{11}.AC=\frac{7}{11}.28=\frac{196}{11}\)cm

Theo định lí Pytago cho tam giác ABC vuông tại A

\(BC=\sqrt{AB^2+AC^2}=\sqrt{\left(\frac{196}{11}\right)^2+28^2}=33,188...\)cm

b, tanC = 5/7 => \(\frac{AC}{AB}=\frac{5}{7}\Rightarrow AB=\frac{7}{5}AC=\frac{7}{5}.28=\frac{196}{5}\)cm

Theo định lí Pytago tam giác ABC vuông tại A

\(BC=\sqrt{AB^2+AC^2}=\sqrt{\left(\frac{196}{5}\right)^2+28^2}=\frac{28\sqrt{74}}{5}\)cm

c, cosC = 4/5 => \(\frac{AC}{BC}=\frac{4}{5}\Rightarrow BC=\frac{5}{4}AC=\frac{5}{4}.28=35\)cm

Theo định lí Pytago tam giác ABC vuông tại A

\(AB=\sqrt{BC^2-AC^2}=21\)cm

d, sinC = 3/5 => \(\frac{AB}{BC}=\frac{3}{5}\Rightarrow\frac{AB}{3}=\frac{BC}{5}\Rightarrow\frac{BC^2}{25}=\frac{AB^2}{9}\)

Theo tính chất dãy tỉ số bằng nhau

\(\frac{BC^2}{25}=\frac{AB^2}{9}=\frac{BC^2-AB^2}{25-9}=\frac{AC^2}{16}=49\)

\(\Rightarrow BC=35cm;AB=21cm\)