Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C.
Đặt t = sin x , t ∈ − 1 ; 1 . Phương trình đã cho trở thành 2 t + 1 t + 2 = m (*).
Để phương trình đã cho có đúng hai nghiệm thuộc đoạn 0 ; π thì phương trình (*) phải có đúng một nghiệm thuộc nửa khoảng 0 ; 1 .
Xét hàm số f t = 2 t + 1 t + 2 . Ta có f ' t = 3 t + 2 2 .
Bảng biến thiên của :
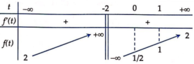
Vậy để phương trình (*) có đúng một nghiệm thuộc nửa khoảng 0 ; 1 thì m ∈ 1 2 ; 1 . Vậy C là đáp án đúng

Đáp án B
Ta có y ' = 4 sin 2 x cos x sin x - ( 2 m 2 - 5 m + 2 ) cos x = cos x [ ( 2 sin x - 1 ) 2 - ( 2 m 2 - 5 m + 3 ) ]
Xét trên ( 0 ; π 2 ) ta thấy cos x > 0 , để hàm số đồng biến trên khoảng này thì ( 2 sin x - 1 ) 2 - ( 2 m 2 - 5 m + 3 ) ≥ 0 với ∀ x ∈ ( 0 ; π 2 ) hay ( 2 m 2 - 5 m + 3 ) ≤ 0 ⇒ 1 ≤ m ≤ 3 2 do m nguyên nên tồn tại duy nhất m=1

Đặt t = sinx do ![]()
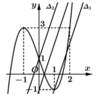
● Gọi ∆ 1 là đường thẳng qua điểm (1;-1) và song song với đường thẳng y = 3x nên có phương trình y = 3x - 4
● Gọi ∆ 2 là đường thẳng qua điểm (0;1) và song song với đường thẳng y = 3x nên có phương trình y = 3x+1
Do đó phương trình
f
sin
x
=
3
sin
x
+
m
có nghiệm thuộc khoảng
0
;
π
khi và chỉ khi phương trình f(t) = 3t + m có nghiệm thuộc nửa khoảng ![]() Chọn A.
Chọn A.







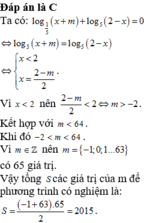
Đáp án A
Phương pháp giải:
Biến đổi công thức lượng giác, đưa phương trình bài cho về dạng phương trình cơ bản, kết hợp với điều kiện nghiệm để tìm giá trị của tham số m
Lời giải: