Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng BĐT tam giác ta có:
a+b>c =>c-a<b =>c2-2ac+a2<b2
a+c>b =>b-c <a =>b2-2bc+c2<a2
b+c>a =>a-b<c =>a2-2ab+b2<c2
Suy ra: c2-2ac+a2+b2-2bc+c2+a2-2ab+b2<a2+b2+c2
<=>-2.(ab+bc+ca)+2.(a2+b2+c2)<a2+b2+c2
<=>-2(ab+bc+ca)<-(a2+b2+c2)
<=>2.(ab+bc+ca)<a2+b2+c2

vì (C) đi qua điểm A nên tọa độ điểm A thỏa mãn pt \(y=\frac{ax^2-bx}{x-1}\) ta có \(\frac{5}{2}=\frac{a+b}{-2}\Rightarrow a+b=-5\)
vì tiếp tuyến của đồ thị tại điểm O có hệ số góc =-3 suy ra y'(O)=-3
ta có \(y'=\frac{ax^2-2ax+b}{\left(x-1\right)^2}\) ta có y'(O)=b=-3 suy ra a=-2
vậy ta tìm đc a và b

a: Xét tứ giác OBDC có
\(\widehat{OBD}+\widehat{OCD}=180^0\)
Do đó: OBDC là tứ giác nội tiếp
b: Xét ΔEBA và ΔECB có
\(\widehat{E}\) chung
\(\widehat{EAB}=\widehat{EBC}\)
Do đó: ΔEBA\(\sim\)ΔECB
Suy ra: EB/EC=EA/EB
hay \(EB^2=EC\cdot EA\)

ta có \(\left|x-a\right|+\left|x-b\right|+\left|x-c\right|+\left|x-d\right|\ge\left|\left(x-a\right)+\left(x-b\right)+\left(c-x\right)+\left(d-x\right)\right|=\left|c+d-a-b\right|=c+d-a-b\)( do a<b<c<d => c-a>0 và d-b>0)
vậy Min A= c+d-a-b

Ta có:
7/12 = 4/12 + 3/12 = 1/3 + 1/4 = 20/60 + 20/80
và 1/41 + 1/42 + 1/43 +...+ 1/79 + 1/80 = (1/41 + 1/42 + 1/43 + ...+ 1/60) + (1/61 + 1/62 +...+ 1/79 + 1/80)
Do 1/41> 1/42 > 1/43 > ...>1/59 > 1/60
=> (1/41 + 1/42 + 1/43 + ...+ 1/60) > 1/60 + ...+ 1/60 = 20/60
và 1/61> 1/62> ... >1/79> 1/80
=> (1/61 + 1/62 +...+ 1/79 + 1/80) > 1/80 + ...+ 1/80 = 20/80
Vậy 1/41 + 1/42 + 1/43 +...+ 1/79 + 1/80 > 20/60 + 20/80 = 7/12

Phương pháp:
Xác định tâm đường tròn ngoại tiếp O, O ' của hai tam giác đáy. Khi đó, tâm mặt cầu ngoại tiếp hình lăng trụ là trung điểm của OO’.
Cách giải:
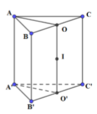
Do tam giác ABC vuông cân tại A nên trung điểm O của BC là tâm đường tròn ngoại tiếp tam giác ABC.
Tương tự, trung điểm O’ của B’C’ là tâm đường tròn ngoại tiếp tam giác A’B’C’.
Khi đó, tâm mặt cầu I ngoại tiếp hình lăng trụ là trung điểm của OO’.




Đáp án C
Tam giác ABC vuông tại A ⇒ B C = A B 2 + A C 2 = 2 a ⇒ R Δ A B C = B C 2 = a
Bán kính mặt cầu ngoại tiếp khối lăng trụ là R = R 2 Δ A B C + A A ' 2 4 = a 2 + 2 a 2 4 = a 2 .