PT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
SG
2
LH
22 tháng 5 2017
Cho 3 điểm k thẳng hàng A , B, C . Vẽ các đoạn thẳng AB, BC , CA. Vẽ đường thẳng a cắt AC , BC tương ứng tại D , E
AN
9 tháng 6 2017
đề 1: vẽ 3 đoạn thẳng sao cho mỗi đoạn thẳng cắt hai đoạn thẳng cobf lại tại đầu mút của chúng, rồi vẽ đường thẳng a cắt hai đoạn trong 3 đoạn thẳng đó. Đặt tên cho các giao điểm.
đề 2: cho 3 điểm không thẳng hàng A, B, C . Vẽ các đoạn thẳng AB, BC, CA. Vẽ đường thẳng a cắt AC và BC tương ứng tại D và E
23 tháng 9 2016
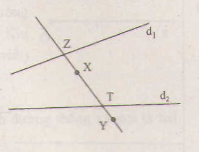
Ba điểm X,Z,T thẳng hàng vậy X nằm trên đường thẳng ZT.
– Ba điểm Y,Z,T thẳng hàng vì vậy Y nằm trên đường thẳng ZT.
Suy ra X,Y nằm trên đường thẳng ZT, dó đó 4 điểm Z,Y,Z,T thẳng hàng.
23 tháng 9 2016
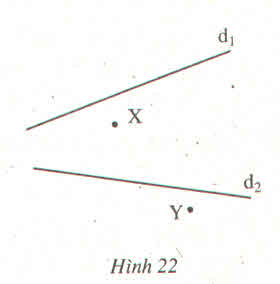
nối hai điểm X,Y kéo dài lại với nhau X,Ycắt d2 tai z ,X,Y căt d2 tại T
13 tháng 5 2022
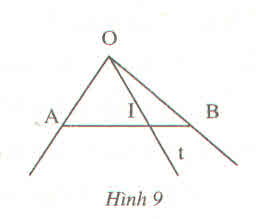
a: Trên hình có 3 góc, đó là các góc xOy;yOz; xOz
b: Trên cùng một nửa mặt phẳng bờ chứa tia Ox, ta có: \(\widehat{xOy}< \widehat{xOz}\)
nên tia Oy nằm giữa hai tia Ox và Oz
mà \(\widehat{xOy}=\dfrac{1}{2}\widehat{xOz}\)
nên Oy là phân giác của góc xOz
c: \(\widehat{zOx'}=180^0-120^0=60^0\)
13 tháng 10 2016
Sơ đồ minh họa:
A B C G D E
\(S_{BCD}=\frac{1}{3}S_{ABC}\) (1) ( Chung chiều cao hạ từ \(C\) xuống \(AB\) và có đáy \(BD=\frac{1}{3}=AB\) do \(AD\) gấp đôi \(DB\) ). \(S_{BCE}=\frac{1}{3}S_{ABC}\) (2) ( Chung chiều cao hạ từ \(B\) xuống \(AC\) và có đáy \(EC=\frac{1}{3}AC\) do \(AE\) gấp đôi \(EC\) ).
Từ (1) và (2) \(\Rightarrow\) \(S_{BCD}=S_{BCE}\)
\(S_{BCD}-S_{BGC}=S_{GDB}\); \(S_{BCE}-S_{BGC}=S_{GEC}\)
Do đó \(S_{GDB}=S_{GEC}\)
G
23 tháng 1 2019
a) Ta chia hình vuông thành 4 phần bằng nhau, sau đó tô 1 phần:
b) Ta chia hình chữ nhật ra 3 phần bằng nhau, sau đó tô 2 phần:
. ai làm được mình sẽ tick.10 lần
5 tháng 8 2016
Ta có định lí :
Một điểm trên một đường thẳng thì có hai tia đối nhau.
Vậy theo đề bài ta có :
5 . 2 = 10 (cặp)
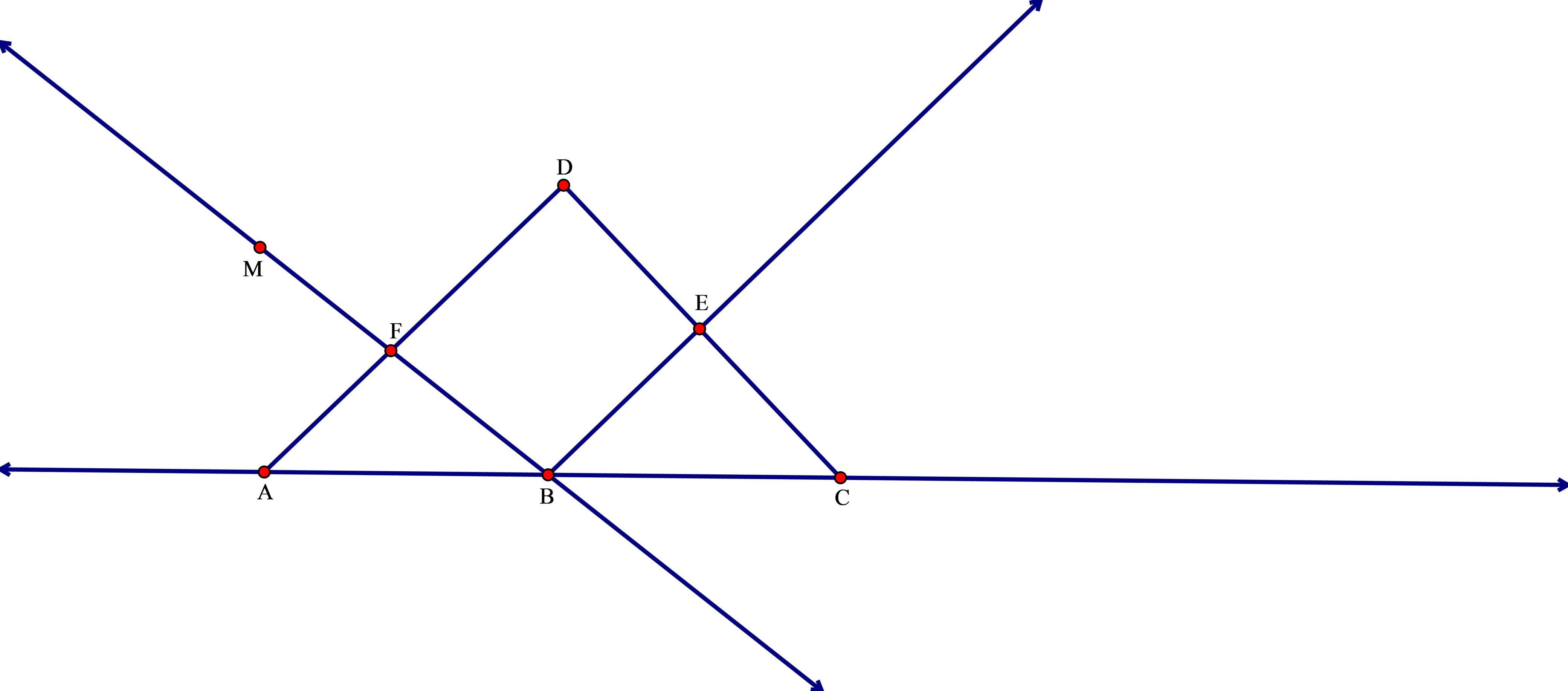
Vẽ đường thẳng đi qua ba điểm A, B, C thẳng hàng trong đó B nằm giữa A và C. Lấy điểm D nằm ngoài đường thẳng đó. Vẽ các đoạn thẳng DA và DC. Vẽ tia BE cắt đoạn thẳng DC tại E. Lấy điểm M nằm khác phía với điểm B bờ là đoạn thẳng AD, vẽ đường thẳng BM cắt đoạn thẳng AD tại E.