Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C.
Ta có:
S t p = 2 S x q ⇔ 2 π R h + 2 π R 2 = 4 π R h ⇔ R = h .

Chọn A.
Phương pháp:
Công thức tính diện tích xung quanh của hình trụ:

Hình trụ đó có diện tích toàn phần gấp ba diện tích xung quanh nên ta có:


vì (C) đi qua điểm A nên tọa độ điểm A thỏa mãn pt \(y=\frac{ax^2-bx}{x-1}\) ta có \(\frac{5}{2}=\frac{a+b}{-2}\Rightarrow a+b=-5\)
vì tiếp tuyến của đồ thị tại điểm O có hệ số góc =-3 suy ra y'(O)=-3
ta có \(y'=\frac{ax^2-2ax+b}{\left(x-1\right)^2}\) ta có y'(O)=b=-3 suy ra a=-2
vậy ta tìm đc a và b

Theo công thức ta có:
Sxq = 2πrh = 2√3 πr2
Stp = 2πrh + 2πr2 = 2√3 πr2 + 2 πr2 = 2(√3 + 1)πr2 ( đơn vị thể tích)
b) Vtrụ = πR2h = √3 π r3
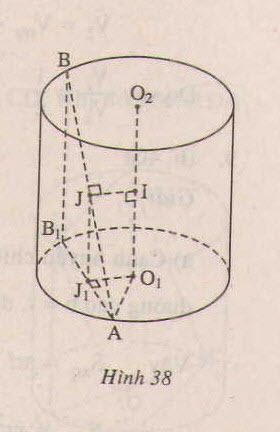
c) Giả sử trục của hình trụ là O1O2 và A nằm trên đường tròn tâm O1, B nằm trên đường tròn tâm O2; I là trung điểm của O1O2, J là trung điểm cảu AB. Khi đó IJ là đường vuông góc chung của O1O2 và AB. Hạ BB1 vuông góc với đáy, J1 là hình chiếu vuông góc của J xuống đáy.
Ta có là trung điểm của
,
= IJ.
Theo giả thiết = 300.
do vậy: AB1 = BB1.tan 300 = = r.
Xét tam giác vuông
AB1 = BB1.tan 300 = O1J1A vuông tại J1, ta có: =
-
.
Vậy khoảng cách giữa AB và O1O2 :

hoành độ giao điểm là nghiệm của pt
\(x^3-3mx^2+3\left(2m-1\right)x+1=2mx-4m+3\Leftrightarrow x^3-3mx^2+4mx-3x-2+4m=0\Leftrightarrow x^3-3x-2-m\left(3x^2-4x+4\right)=0\)
giải hệ pt ta có \(C_m\) luôn đi qua điểm A là nghiệm của hệ pt sau
\(\begin{cases}3x^2-4x+4=0\\x^3-3x-2=0\end{cases}\)
ta đc điều phải cm

Chọn đáp án C.