Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D.
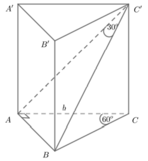
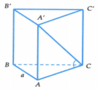
Phương pháp : Xác định góc. Diện tích xung quanh hình lăng trụ đứng bằng chu vi đáy nhân với chiều cao. Từ đó xác định chu vi đáy và chiều cao.

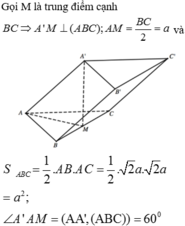
Vậy diện tích xung quanh hình lăng trụ là

Bài 3:
Do a và b đều không chia hết cho 3 nhưng khi chia cho 3 thì có cùng số dư nên\(\left[{}\begin{matrix}\left\{{}\begin{matrix}a=3n+1\\b=3m+1\end{matrix}\right.\\\left\{{}\begin{matrix}a=3n+2\\b=3m+2\end{matrix}\right.\end{matrix}\right.\)
TH1:\(\left\{{}\begin{matrix}a=3n+1\\b=3m+1\end{matrix}\right.\)
\(\Rightarrow ab-1=\left(3n+1\right)\left(3m+1\right)-1\)
\(\Rightarrow ab-1=9nm+3m+3n+1-1=9nm+3m+3n⋮3\) nên là bội của 3 (đpcm)
TH2:\(\left\{{}\begin{matrix}a=3n+2\\b=3m+2\end{matrix}\right.\)
\(\Rightarrow ab-1=\left(3n+2\right)\left(3m+2\right)-1\)
\(\Rightarrow ab-1=9nm+6m+6n+4-1=9nm+6m+6n+3⋮3\) nên là bội của 3 (đpcm)
Vậy ....
Bài 2:
\(B=\frac{1}{2010.2009}-\frac{1}{2009.2008}-\frac{1}{2008.2007}-...-\frac{1}{3.2}-\frac{1}{2.1}\)
\(\Rightarrow B=\frac{1}{2010.2009}-\left(\frac{1}{2009.2008}+\frac{1}{2008.2007}+...+\frac{1}{3.2}+\frac{1}{2.1}\right)\)
Đặt A=\(\frac{1}{2009.2008}+\frac{1}{2008.2007}+...+\frac{1}{3.2}+\frac{1}{2.1}\)
\(\Rightarrow A=\frac{2009-2008}{2009.2008}+\frac{2008-2007}{2008.2007}+...+\frac{3-2}{3.2}+\frac{2-1}{2.1}\)
\(\Rightarrow A=\frac{2-1}{2.1}+\frac{3-2}{3.2}+...+\frac{2008-2007}{2008.2007}+\frac{2009-2008}{2009.2008}\)
\(\Rightarrow A=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+...+\frac{1}{2007}-\frac{1}{2008}+\frac{1}{2008}-\frac{1}{2009}\)
\(\Rightarrow A=1-\frac{1}{2009}\)
\(\Rightarrow B=\frac{1}{2010.2009}-A=\frac{1}{2010.2009}-\left(1-\frac{1}{2009}\right)\)
\(\Rightarrow B=\frac{1}{2010.2009}+\frac{1}{2009}-1=\frac{2011}{2010.2009}-1\)

a) Ta có: góc FAB + góc BAC = 90 độ
góc EAC + góc BAC = 90 độ
=> Góc FAB = góc EAC
AF=AC; AB=AE
=> Tam giác AFB = tam giác ACE
=> FB=EC
b) Lấy K sao cho M là trung điểm của AK thì ta có ACKB là hình bình hành nên góc ACB =180* - góc BAC. Ta cũng tính dc góc FAE= 180* - góc BAC ( tổng của BAC với 2 lần góc CAE, mà góc CAE=90* -góc BAC). Thêm với AC=AF , CK=AE (=AB) nên tam giác ACK = tam giác FAE nên AK=EF mà AK=2AM nên EF=2AM
c) Gọi H là giao của AM và EF. Tam giác ACK = tam giác FAE nên góc CAK = góc AFE, mà góc CAK phụ với góc MAF nên góc AFE cũng phụ góc MAF. Xét trong tam giác AHF có góc F và góc A phụ nhau nên tam giác AHF vuông tại H suy ra AM vuông góc với EF.

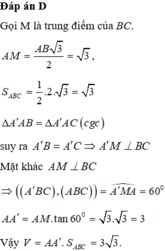
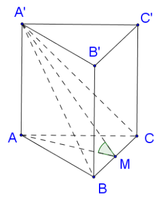
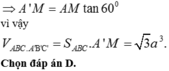

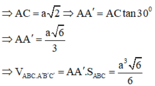
Đáp án B
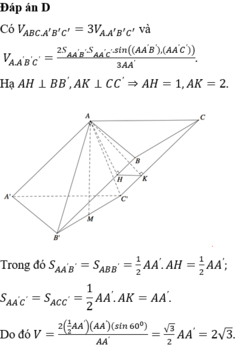
Vậy diện tích xung quanh của lăng trụ đứng ABCA′B′C′ là