Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C D O
ABCD là hcn có AC cắt BD tại O
=> O là trung điểm của BD
=> OD = 1/2BD
có \(\frac{AD}{OD}=\frac{6}{5}\Rightarrow\frac{AD}{\frac{1}{2}BD}=\frac{6}{5}\text{ hay }\frac{AD}{BD}=\frac{6}{10}\)
\(\Rightarrow\hept{\begin{cases}AD=6x\\BD=10x\end{cases}\left(x>0\right)}\)
xét tam giác ABD có ^BAD = 90 \(\Rightarrow AD^2+AB^2=BD^2\left(pytago\right)\)
\(\Rightarrow\left(6x\right)^2+AB^2=\left(10x\right)^2\)
\(\Rightarrow AB=8x\)
có AB + AD = 14 : 2 = 7
=> 8x + 6x = 7
=> 14x = 7
=> x = 1/2
=> AB = 4

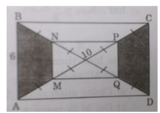
a) Ta có MN và PQ lần lượt là các đường trung bình của các tam giác AOB và COD mà AB // CD và AB = CD nên MN // PQ và MN = PQ
⇒ Tứ giác MNPQ là hình bình hành.
Tương tự NP // BC mà AB ⊥ BC nên MN ⊥ NP. Do đó MNPQ là hình chữ nhật.
Trong ΔABC ta có

Vậy SMNPQ = MN.PQ = 3.4 = 12 (cm2).
b)Dễ thấy ΔAOB = ΔCOD (c.c.c).
Tương tự ΔMON = ΔPOQ
Do đó: SAOB = SCOD và SMON = SPOQ.
⇒ SAOB - SMON = SCOD - SPOQ hay SAMNB = SCPQD.

Áp dụng địnhlý Pytago, ta tính được AB = 24cm. Vì M, N, P, Q lần lượt là trung điểm của OA, OB, OC, OD nên sử dụng tính chất của các đường trung bình, ta chứng minh được MNNPQ là hình chữ nhật.
Đồng thời, ta có: M N = 1 2 A B = 12 c m , M Q = 1 2 A D = 3 , 5 c m
Þ SMNPQ = MN.MQ = 42cm2