Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
+TXĐ: X\(\in\)R
+y'=\(3x^2-6x\Rightarrow y'=0\Leftrightarrow\int_{x=2;y=0}^{x=0;y=4}\)
+y''=6(x-1)=> y' = 0 khi x = 1;y=2
+
| x | -\(\infty\) 0 1 2 +\(\infty\) |
| y' | + 0 - - 0 + |
| y |
Tập xác định : D = [0 ; 2]; y' = , ∀x ∈ (0 ; 2); y' = 0 ⇔ x = 1.
Bảng biến thiên :
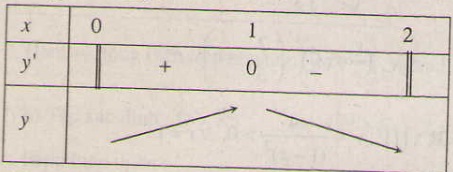
Vậy hàm số đồng biến trên khoảng (0 ; 1) và nghịch biến trên khoảng (1 ; 2).
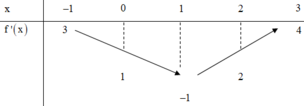
Tập xác định : D = R. y' = => y' = 0 ⇔ x=-1 hoặc x=1.
Bảng biến thiên :
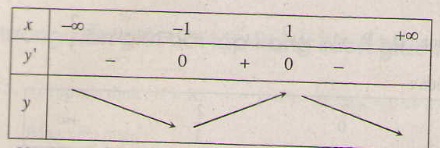
Vậy hàm số đồng biến trên khoảng (-1 ; 1); nghịch biến trên các khoảng (-∞ ; -1), (1 ; +∞).
ta có \(y'=\frac{mx^2+4mx+14}{\left(x+2\right)^2}\) để hàm số nghịch biến trên \(\left(1;+\infty\right)\) thì y'<0 với mọi x thuộc khoảng đó suy ra
\(\begin{cases}m<0\\\Delta=4m^2-14m<0\end{cases}\)
giải ra ta đc đkcủa m
Chọn D.
Dựa vào bảng biến thiên suy ra hàm số nghịch biến trên (0;1)
a) TXĐ: D = [0; + \(\infty\))
\(y'=1+\frac{1}{2\sqrt{x}}\) > 0 với mọi x thuộc D
BBT: x y' y 0 +oo + 0 +oo
Từ BBT => Hàm số đồng biến trên D ;
y đạt cực tiểu bằng 0 tại x = 0
Hàm số không có cực đại
b) TXĐ : D = = [0; + \(\infty\))
\(y'=1-\frac{1}{2\sqrt{x}}\)
\(y'=0\) <=> \(2\sqrt{x}=1\) <=> \(x=\frac{1}{4}\)
x y' y 0 +oo + 0 +oo -1/4 1/4 0 -
Từ BBT: Hàm số đồng biến trên (1/4; + \(\infty\)); nghịch biến trên (0;1/4)
Hàm số đạt cực tiểu = -1/4 tại x = 1/4
Hàm số không có cực đại
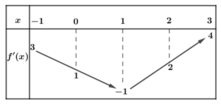
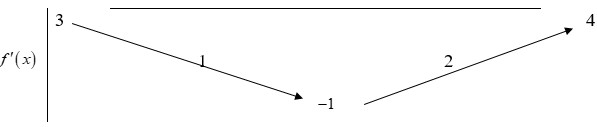
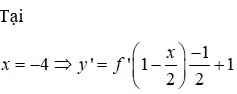
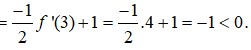
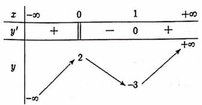
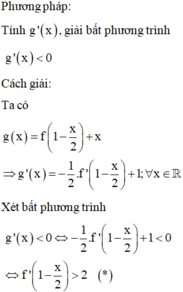
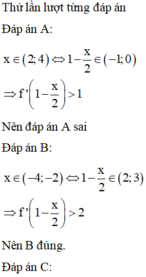
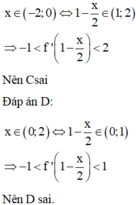
Ta có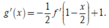
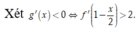
= TH1: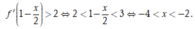
Do đó hàm số nghịch biến trên (-4;-2)
= TH2: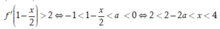
nên hàm số chỉ nghịch biến trên khoảng (2-2a;4) chứ không nghịch biến trên toàn khoảng (2;4)
Vậy hàm số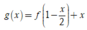
nghịch biến trên (-4;-2)
Chọn A.