Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

7.
Thể tích:
\(V=\pi\int\limits^{\frac{\pi}{2}}_0sin^2xdx=\frac{\pi}{2}\int\limits^{\frac{\pi}{2}}_0\left(1-cos2x\right)dx=\frac{\pi}{2}\left(x-\frac{1}{2}sin2x\right)|^{\frac{\pi}{2}}_0=\frac{\pi^2}{4}\)
8.
\(z=\frac{z-17i}{5-i}\Leftrightarrow\left(5-i\right)z=z-17i\)
\(\Leftrightarrow z\left(i-4\right)=17i\Rightarrow z=\frac{17i}{i-4}=1-4i\)
Rốt cuộc câu này hỏi modun hay phần thực vậy ta?
Phần thực bằng 1
Môđun \(\left|z\right|=\sqrt{17}\)
9.
\(\left(1-3i\right)z=8+6i\Rightarrow z=\frac{8+6i}{1-3i}=-1+3i\)
\(\Rightarrow\left|z\right|=\sqrt{\left(-1\right)^2+3^2}=\sqrt{10}\)
10.
\(\left(1+i\right)^2\left(2-i\right)z=8+i+\left(1+2i\right)z\)
\(\Leftrightarrow2i\left(2-i\right)z-\left(1+2i\right)z=8+i\)
\(\Leftrightarrow\left(4i+2-1-2i\right)z=8+i\)
\(\Leftrightarrow z=\frac{8+i}{2i+1}=2-3i\)
Phần thực \(a=2\)
11.
Điểm biểu diễn số phức là điểm có tọa độ \(\left(-1;-2\right)\)
4.
\(I=\int\limits^{\frac{\pi}{2}}_{\frac{\pi}{4}}\frac{dx}{sin^2x}=-cotx|^{\frac{\pi}{2}}_{\frac{\pi}{4}}=1\)
5.
\(I=\int\limits^a_2\frac{2x-1}{1-x}dx=\int\limits^a_2\left(-2-\frac{1}{x-1}\right)dx=\left(-2x-ln\left|x-1\right|\right)|^a_2=-2a-ln\left|a-1\right|+4\)
\(\Rightarrow-2a+4-ln\left|a-1\right|=-4-ln3\Rightarrow a=4\)
6.
Phương trình hoành độ giao điểm:
\(x^3=x^5\Rightarrow\left[{}\begin{matrix}x=0\\x=1\\x=-1\end{matrix}\right.\)
Diện tích hình phẳng:
\(S=\int\limits^0_{-1}\left(x^5-x^3\right)dx+\int\limits^1_0\left(x^3-x^5\right)dx=\frac{1}{6}\)

a) f(x) = 2x3 – 3x2 – 12x + 1 ⇒ f’(x) = 6x2 – 6x – 12
f’(x) = 0 ⇔ x ∈ {-1, 2}
So sánh các giá trị:
f(x) = -3; f(-1) = 8;
f(2) = -19, f(52)=−332f(52)=−332
Suy ra:
maxx∈[−2,52]f(x)=f(−1)=8minx∈[−2,52]f(x)=f(2)=−19maxx∈[−2,52]f(x)=f(−1)=8minx∈[−2,52]f(x)=f(2)=−19
b) f(x) = x2 lnx ⇒ f’(x)= 2xlnx + x > 0, ∀ x ∈ [1, e] nên f(x) đồng biến.
Do đó:
maxx∈[1,e]f(x)=f(e)=e2minx∈[1,e]f(x)=f(1)=0maxx∈[1,e]f(x)=f(e)=e2minx∈[1,e]f(x)=f(1)=0
c) f(x) = f(x) = xe-x ⇒ f’(x)= e-x – xe-x = (1 – x)e-x nên:
f’(x) = 0 ⇔ x = 1, f’(x) > 0, ∀x ∈ (0, 1) và f’(x) < 0, ∀x ∈ (1, +∞)
nên:
maxx∈[0,+∞)f(x)=f(1)=1emaxx∈[0,+∞)f(x)=f(1)=1e
Ngoài ra f(x) = xe-x > 0, ∀ x ∈ (0, +∞) và f(0) = 0 suy ra
maxx∈[0,+∞)f(x)=f(0)=0maxx∈[0,+∞)f(x)=f(0)=0
d) f(x) = 2sinx + sin2x ⇒ f’(x)= 2cosx + 2cos2x
f’(x) = 0 ⇔ cos 2x = -cosx ⇔ 2x = ± (π – x) + k2π
⇔ x∈{−π+k2π;π3+k2π3}x∈{−π+k2π;π3+k2π3}
Trong khoảng [0,3π2][0,3π2] , phương trình f’(x) = 0 chỉ có hai nghiệm là x1=π3;x2=πx1=π3;x2=π
So sánh bốn giá trị : f(0) = 0; f(π3)=3√32;f(π)=0;f(3π2)=−2f(π3)=332;f(π)=0;f(3π2)=−2
Suy ra:
maxx∈[0,3π2]f(x)=f(π3)=3√32minx∈[0,3π2]f(x)=f(3π2)=−2




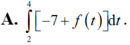
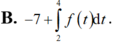
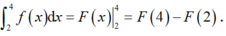
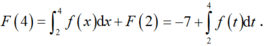
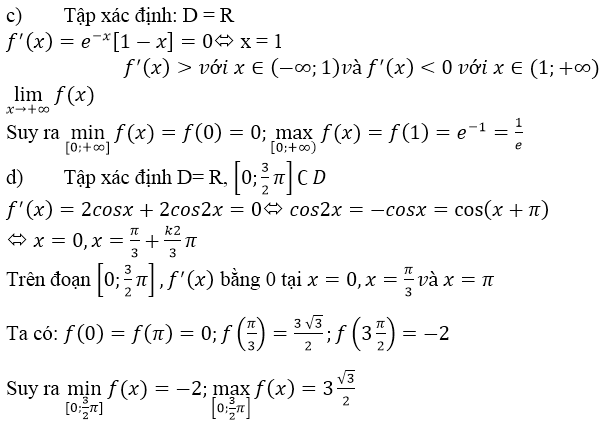
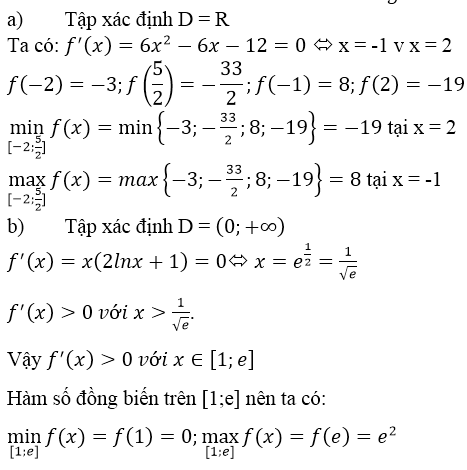
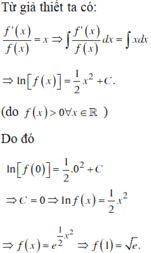
Đáp án C