Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

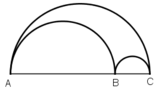
Gọi C 1 , C 2 , C 3 lần lượt là độ dài của các nửa đường tròn đường kính AC, AB, BC, ta có:
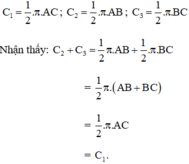
Vậy độ dài của nửa đường tròn đường kính AC bằng tổng các độ dài của hai nửa đường tròn đường kính AB và BC.
Kiến thức áp dụng
+ Độ dài đường tròn đường kính d là: C = π.d
⇒ Độ dài nửa đường tròn đường kính d là: C’ = π.d/2.

Hướng dẫn giải:
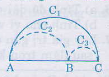
Gọi C1, C2, C3 lần lượt là độ dài của các nửa đường tròn đường kính AC, AB, BC, ta có:
C1 = π. AC (1)
C2 = π.AB (2)
C3 = π.BC (3)
So sánh (1), (2), (3) ta thấy:
C2 + C3 = π(AB +BC) = π. AC (vì B, nằm giữa A, C).
Vậy C1 = C2+C3.

Gọi C1, C2, C3 lần lượt là độ dài của các nửa đường tròn đường kính AC, AB, BC, ta có:
C1 = π. AC (1)
C2 = π.AB (2)
C3 = π.BC (3)
So sánh (1), (2), (3) ta thấy:
C2 + C3 = π(AB +BC) = π. AC (vì B, nằm giữa A, C).
Vậy C1 = C2+C3.

Hướng dẫn giải:
Chu vi bánh xe sau: π x 1,672 (m)
Chu vi bánh xe trước: π x 0,88 (m)
Khi bánh xe sau lăn được 10 vòng thì quãng đường đi được là:
π x 1,672 (m)
Khi đó số vòng lăn của bánh xe trước là:
= 19 vòng
>>>>> Bí kíp học tốt các môn lớp 9 2017 bởi các Thầy Cô uy tín, nổi tiếng học hiệu quả, dễ hiểu
Xem thêm tại: http://loigiaihay.com/bai-69-trang-95-sgk-toan-lop-9-tap-2-c44a6094.html#ixzz4ae4SF8ZI
Hướng dẫn giải:
Gọi C1, C2, C3 lần lượt là độ dài của các nửa đường tròn đường kính AC, AB, BC, ta có:
C1 = π. AC (1)
C2 = π.AB (2)
C3 = π.BC (3)
So sánh (1), (2), (3) ta thấy:
C2 + C3 = π(AB +BC) = π. AC (vì B, nằm giữa A, C).
Vậy C1 = C2+C3.
Xem thêm tại: http://loigiaihay.com/bai-68-trang-95-sgk-toan-lop-9-tap-2-c44a6076.html#ixzz4ae4ixGms

a) Ta có \(\widehat{BOM}=sđ\stackrel\frown{BM}\) (đ/lí góc ở tâm)
Mà \(\stackrel\frown{BM}=120^o=>\widehat{BOM}=120^o\)
Vì \(\widehat{BOM}+\widehat{AOM}=180^o=>\widehat{AOM}=60^o\)
Xét \(\Delta AOM\) có
OA = OM (bán kính)
\(\widehat{AOM}=60^o\left(cmt\right)\)
\(=>\Delta OAM\) đều (dhnb tam giác đều)
b) +) Ta có \(\widehat{AMB}=90^o\) (góc nội tiếp chắn nửa đường tròn)
mà \(\Delta OAM\) đều (cmt) \(=>\widehat{OAM}=60^o\)
\(=>\widehat{ABM}=30^o\)
+) Vì R = 3 cm (gt) => OA = OB = 3 cm => AB = 6cm
Xét \(\Delta AMB\) vg tại A
\(=>AB^2=AM^2+BM^2\)
\(=>6^2=3^2+BM^2\)
\(=>BM=3\sqrt{3}\)


Gọi C1, C2, C3 lần lượt là độ dài của các nửa đường tròn đường kính AC, AB, BC, ta có:
Vậy độ dài của nửa đường tròn đường kính AC bằng tổng các độ dài của hai nửa đường tròn đường kính AB và BC.
Kiến thức áp dụng