Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hướng dẫn giải:
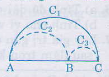
Gọi C1, C2, C3 lần lượt là độ dài của các nửa đường tròn đường kính AC, AB, BC, ta có:
C1 = π. AC (1)
C2 = π.AB (2)
C3 = π.BC (3)
So sánh (1), (2), (3) ta thấy:
C2 + C3 = π(AB +BC) = π. AC (vì B, nằm giữa A, C).
Vậy C1 = C2+C3.

Gọi C1, C2, C3 lần lượt là độ dài của các nửa đường tròn đường kính AC, AB, BC, ta có:
C1 = π. AC (1)
C2 = π.AB (2)
C3 = π.BC (3)
So sánh (1), (2), (3) ta thấy:
C2 + C3 = π(AB +BC) = π. AC (vì B, nằm giữa A, C).
Vậy C1 = C2+C3.

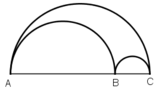
Gọi C 1 , C 2 , C 3 lần lượt là độ dài của các nửa đường tròn đường kính AC, AB, BC, ta có:
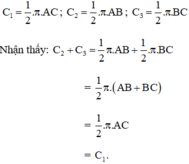
Vậy độ dài của nửa đường tròn đường kính AC bằng tổng các độ dài của hai nửa đường tròn đường kính AB và BC.
Kiến thức áp dụng
+ Độ dài đường tròn đường kính d là: C = π.d
⇒ Độ dài nửa đường tròn đường kính d là: C’ = π.d/2.

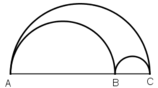
Gọi C1, C2, C3 lần lượt là độ dài của các nửa đường tròn đường kính AC, AB, BC, ta có:
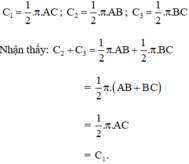
Vậy độ dài của nửa đường tròn đường kính AC bằng tổng các độ dài của hai nửa đường tròn đường kính AB và BC.
Kiến thức áp dụng

Hướng dẫn giải:
Chu vi bánh xe sau: π x 1,672 (m)
Chu vi bánh xe trước: π x 0,88 (m)
Khi bánh xe sau lăn được 10 vòng thì quãng đường đi được là:
π x 1,672 (m)
Khi đó số vòng lăn của bánh xe trước là:
= 19 vòng
>>>>> Bí kíp học tốt các môn lớp 9 2017 bởi các Thầy Cô uy tín, nổi tiếng học hiệu quả, dễ hiểu
Xem thêm tại: http://loigiaihay.com/bai-69-trang-95-sgk-toan-lop-9-tap-2-c44a6094.html#ixzz4ae4SF8ZI
Hướng dẫn giải:
Gọi C1, C2, C3 lần lượt là độ dài của các nửa đường tròn đường kính AC, AB, BC, ta có:
C1 = π. AC (1)
C2 = π.AB (2)
C3 = π.BC (3)
So sánh (1), (2), (3) ta thấy:
C2 + C3 = π(AB +BC) = π. AC (vì B, nằm giữa A, C).
Vậy C1 = C2+C3.
Xem thêm tại: http://loigiaihay.com/bai-68-trang-95-sgk-toan-lop-9-tap-2-c44a6076.html#ixzz4ae4ixGms

Giải thích các bước giải:
a.Ta có AB,ACAB,AC là đường kính của các đường tròn
→AM⊥BM,AN⊥CN→AM⊥BM,AN⊥CN
→ˆPMA=ˆANP=90o→PMA^=ANP^=90o
→AMNP→AMNP nội tiếp đường tròn đường kính APAP
→ˆAPB=ˆAPM=ˆANM=ˆANH=90o−ˆNAH=90o−ˆNAC=ˆACN=ˆACP→APB^=APM^=ANM^=ANH^=90o−NAH^=90o−NAC^=ACN^=ACP^
Lại có ˆPAB=ˆPACPAB^=PAC^
→ΔAPB∼ΔACP(g.g)→ΔAPB∼ΔACP(g.g)
→APAC=BAAP→APAC=BAAP
→AP2=AB.AC

