Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\dfrac{2}{3}x-70\dfrac{10}{11}:\left(\dfrac{131313}{151515}+\dfrac{131313}{353535}+\dfrac{131313}{636363}+\dfrac{131313}{999999}\right)=-5\\ \Rightarrow\dfrac{2}{3}x-\dfrac{780}{11}:\left(\dfrac{13}{15}+\dfrac{13}{35}+\dfrac{13}{63}+\dfrac{13}{99}\right)=-5\\ \Rightarrow\dfrac{2}{3}x-\dfrac{780}{11}:13\left(\dfrac{1}{15}+\dfrac{1}{35}+\dfrac{1}{63}+\dfrac{1}{99}\right)=-5\\ \Rightarrow\dfrac{2}{3}x-\dfrac{780}{11}:13.\dfrac{4}{33}=-5\\ \Rightarrow\dfrac{2}{3}x-\dfrac{780}{11}:\dfrac{52}{33}=-5\\ \Rightarrow\dfrac{2}{3}x-45=-5\\ \Rightarrow\dfrac{2}{3}x=40\\ \Rightarrow x=60\)

\(l=\dfrac{1}{1.4}+\dfrac{1}{4.7}+\dfrac{1}{7.10}+....+\dfrac{1}{97.100}\)
\(=\dfrac{1}{3}\left(1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{10}+...+\dfrac{1}{97}-\dfrac{1}{100}\right)\)
\(=\dfrac{1}{3}\left(1-\dfrac{1}{100}\right)=\dfrac{1}{3}-\dfrac{1}{300}< \dfrac{1}{3}\left(đpcm\right)\)

\(\left(\dfrac{1}{4.9}+\dfrac{1}{9.14}+\dfrac{1}{14.19}+...+\dfrac{1}{44.49}\right)\)
\(=\) \(\dfrac{1}{4}-\dfrac{1}{9}+\dfrac{1}{9}-\dfrac{1}{14}+\dfrac{1}{14}-\dfrac{1}{19}+...+\dfrac{1}{44}-\dfrac{1}{49}\)
\(=\) \(\dfrac{1}{4}-\dfrac{1}{49}\)
\(=\) \(\dfrac{49}{196}-\dfrac{4}{196}\)
\(=\) \(\dfrac{45}{196}\)
Biểu thức ban đầu không thỏa công thức nên không giải như vậy đc => sai.

Bài 1 :
Sửa để : \(N=\left(\dfrac{1}{4.9}+\dfrac{1}{9.14}+\dfrac{1}{14.19}+....+\dfrac{1}{44.49}\right)\cdot\dfrac{1-3-5-7-..-49}{89}\)
\(N=\dfrac{1}{5}\cdot\left(\dfrac{1}{4}-\dfrac{1}{9}+\dfrac{1}{9}-\dfrac{1}{14}+\dfrac{1}{14}-\dfrac{1}{19}+...+\dfrac{1}{44}-\dfrac{1}{49}\right)\cdot\dfrac{1-\left(3+5+7+..+49\right)}{89}\)
\(N=\dfrac{1}{5}\cdot\left(\dfrac{1}{4}-\dfrac{1}{49}\right)\cdot\dfrac{1-624}{89}\)
\(N=\dfrac{1}{5}\cdot\dfrac{45}{196}\cdot\dfrac{-623}{89}\)
\(\Rightarrow N=\dfrac{9}{196}\cdot-7=\dfrac{-9}{28}\)

Đặt :
\(A=\dfrac{3}{9.14}+\dfrac{3}{14.19}+........+\dfrac{3}{\left(5n-1\right)\left(5n+4\right)}\)
\(\Leftrightarrow\dfrac{5}{3}A=\dfrac{5}{9.14}+\dfrac{5}{14.19}+........+\dfrac{5}{\left(5n-1\right)\left(5n+4\right)}\)
\(\Leftrightarrow\dfrac{5}{3}A=\dfrac{1}{9}-\dfrac{1}{14}+\dfrac{1}{14}-\dfrac{1}{19}+...........+\dfrac{1}{5n-1}-\dfrac{1}{5n+4}\)
\(\Leftrightarrow\dfrac{5}{3}A=\dfrac{1}{9}-\dfrac{1}{5n+4}\)
\(\Leftrightarrow A=\left(\dfrac{1}{9}-\dfrac{1}{5n+4}\right):\dfrac{5}{3}\)
\(\Leftrightarrow A=\left(\dfrac{1}{9}-\dfrac{1}{5n+4}\right).\dfrac{3}{5}\)
\(\Leftrightarrow A=\dfrac{1}{9}.\dfrac{3}{5}-\dfrac{1}{5n+4}.\dfrac{3}{5}\)
\(\Leftrightarrow A=\dfrac{1}{15}-\dfrac{1}{5n+4}.\dfrac{3}{5}< \dfrac{1}{15}\)
\(\Leftrightarrow A< \dfrac{1}{15}\left(đpcm\right)\)
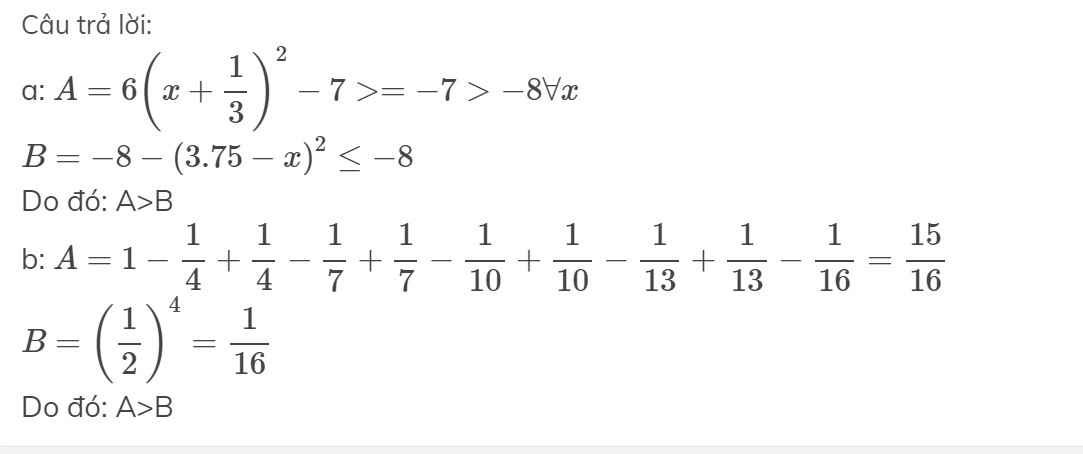
b: Ta có: \(B=\dfrac{1}{4\cdot9}+\dfrac{1}{9\cdot14}+...+\dfrac{1}{64\cdot69}\)
\(=\dfrac{1}{5}\left(\dfrac{5}{4\cdot9}+\dfrac{5}{9\cdot14}+...+\dfrac{5}{64\cdot69}\right)\)
\(=\dfrac{1}{5}\left(\dfrac{1}{4}-\dfrac{1}{9}+\dfrac{1}{9}-\dfrac{1}{14}+...+\dfrac{1}{64}-\dfrac{1}{69}\right)\)
\(=\dfrac{1}{5}\cdot\dfrac{65}{4\cdot69}\)
\(=\dfrac{13}{276}\)
\(A=\dfrac{2}{1\cdot4}+\dfrac{2}{4\cdot7}+...+\dfrac{2}{97\cdot100}\\ A=\dfrac{2}{3}\left(\dfrac{3}{1\cdot4}+\dfrac{3}{4\cdot7}+...+\dfrac{3}{97\cdot100}\right)\\ A=\dfrac{2}{3}\left(1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}+...+\dfrac{1}{97}-\dfrac{1}{100}\right)\\ A=\dfrac{2}{3}\left(1-\dfrac{1}{100}\right)=\dfrac{2}{3}\cdot\dfrac{99}{100}=\dfrac{33}{50}\\ B=\dfrac{1}{4\cdot9}+\dfrac{1}{9\cdot14}+...+\dfrac{1}{64\cdot69}\\ B=\dfrac{1}{5}\left(\dfrac{5}{4\cdot9}+\dfrac{5}{9\cdot14}+...+\dfrac{5}{64\cdot69}\right)\\ B=\dfrac{1}{5}\left(\dfrac{1}{4}-\dfrac{1}{9}+\dfrac{1}{9}-\dfrac{1}{14}+...+\dfrac{1}{64}-\dfrac{1}{69}\right)\\ B=\dfrac{1}{5}\left(\dfrac{1}{4}-\dfrac{1}{69}\right)=\dfrac{1}{5}\cdot\dfrac{65}{276}=\dfrac{13}{276}\)
\(C=70\left(\dfrac{13}{56}+\dfrac{13}{72}+\dfrac{13}{90}\right)=70\cdot13\left(\dfrac{1}{56}+\dfrac{1}{72}+\dfrac{1}{90}\right)\\ C=910\left(\dfrac{1}{7\cdot8}+\dfrac{1}{8\cdot9}+\dfrac{1}{9\cdot10}\right)\\ C=910\left(\dfrac{1}{7}-\dfrac{1}{8}+\dfrac{1}{8}-\dfrac{1}{9}+\dfrac{1}{9}-\dfrac{1}{10}\right)\\ C=910\left(\dfrac{1}{7}-\dfrac{1}{10}\right)=910\cdot\dfrac{3}{70}=39\)