
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




\(\frac{a+7b}{a+5b}=\frac{29}{28}\Rightarrow\left(a+7b\right).28=\left(a+5b\right).29\)
\(\Leftrightarrow28a+196b=29a+145b\)
\(\Leftrightarrow29a-28a=196b-145b\)
\(\Leftrightarrow a=51b\)
Do đó a luôn chia hết cho 51 nên a không thể là số nguyên tố.
Vậy không tìm được số a;b thỏa mãn đề bài.

3a-2b chia hết cho 11 nên 2(4a+b)=8a+2b=11a-(3a-2b) chia hết cho 11.
Suy ra 4a+b chi hết cho 11.
Vậy 2a-5b=22a-5(4a+b) cũng chia hết cho 11
3a-2b chia hết cho 11 nên 2(4a+b)=8a+2b=11a-(3a-2b) chia hết cho 11.
Suy ra 4a+b chi hết cho 11.
Vậy 2a-5b=22a-5(4a+b) cũng chia hết cho 11![]()

Ta có:
\(\frac{a}{b}<\frac{c}{d}\)
\(ad<\)\(bc\)
\(\Rightarrow3ad<\)\(3bc\)
\(\Rightarrow2ab+3ad<2ab+3bc\)
\(\Rightarrow a\left(2b+3d\right)<\)\(b\left(2a+3c\right)\)
\(\Rightarrow\frac{a}{b}<\)\(\frac{2a+3c}{2b+3d}\)
Vậy ...

Đặt \(A=\left|x-2\right|+\left|x-3\right|\)
Ta có:
\(\left|x-3\right|=\left|3-x\right|\)
\(\Rightarrow A=\left|x-2\right|+\left|3-x\right|\ge\left|x-2+3-x\right|=1\)
Do đó 1 chính là giá trị nhỏ nhất của A
Dấu "=" xảy ra khi \(\left(x-2\right)\left(3-x\right)\ge0\)
Ta có bảng xét dấu sau:
x x-2 3-x (x-2)(3-x) 2 3 0 0 + + + + + 0 0 _ _ _ _
\(\Rightarrow2\le\)\(x\le\)\(3\)
\(\Rightarrow x\in\left\{2;3\right\}\)
Vậy \(x\in\left\{2;3\right\}\)
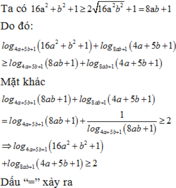
Gọi d là ƯCLN của 11a +2b và 18a +5b => 11a +2b chia hết cho d và 18a +5b chia hết cho d
=> 18.(11a + 2b) chia hết cho d và 11(18a + 5b) chia hết cho d
=> 11(18a + 5b) - 18.(11a + 2b) chia hết cho d => 19b chia hết cho d
=> 19 chia hết cho d hoặc b chia hết cho d
=> d là ước của 19 hoặc d là ước của b
Tương tự ta cũng có 5.(11a + 2b) chia hết cho d và 2(18a + 5b) chia hết cho d
=> 5.(11a + 2b) - 2(18a + 5b) chia hết cho d => 19a chia hết cho d => 19 chia hết cho d hoặc a chia hết cho d => d là ước của 19 hoặc d là ước của a (2)
Từ (1) và (2) suy ra d là ước của 19 hoặc d là ước chung của a và b
=> d = 19 hoặc d = 1
Vậy ƯCLN của 11a + 2b và 18a + 5b là 19 hoặc 1