Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
ta tính \(y'=3x^2-4x+1\)
\(y'=0\Rightarrow3x^2-4x+1=0\Rightarrow x=1;x=\frac{1}{3}\)
ta có
ta có trong khoảng 2 nghiệm thì y' cùng dấu với hệ số a, ngoài khoảng 2 nghiệm trái dấu với hệ số a
suy ra f'(x)>0 với \(x\in\left(-\infty;\frac{1}{3}\right)\cup\left(1;+\infty\right)\) suy ra hàm số đồng biến trên \(\left(-\infty;\frac{1}{3}\right)\cup\left(1;+\infty\right)\)
lại có f'(x)<0 với \(x\in\left(\frac{1}{3};1\right)\) suy ra hàm số nghịch biến trên \(\left(\frac{1}{3};1\right)\)
a) Tập xác định: R; y' = 3(1 - x2); y' = 0 ⇔ x = ± 1 .
Bảng biến thiên :
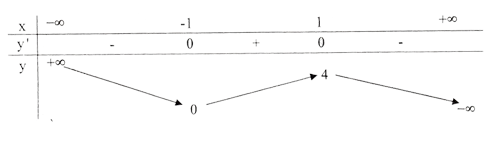
Đồ thị như hình bên.
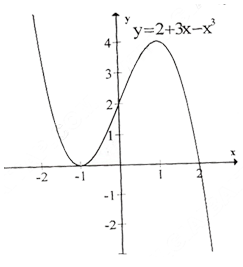
b) Tập xác định : R ; y' = 3x2 + 8x + 4; y' = 0 ⇔ x= -2, x = .png)
.
Bảng biến thiên :
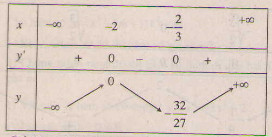
Đồ thị như hình bên.
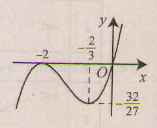
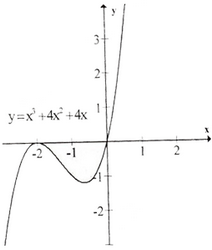
c) Tập xác định : R ;
y' = 3x2 + 2x + 9 > 0, ∀x. Vậy hàm số luôn đồng biến, không có cực trị.
Bảng biến thiên :
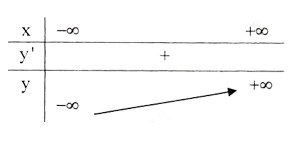
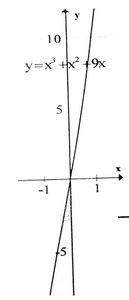
Đồ thị hàm số như hình bên.
d) Tập xác định : R ;
y' = -6x2 ≤ 0, ∀x. Vậy hàm số luôn nghịch biến, không có cực trị.
Bảng biến thiên :
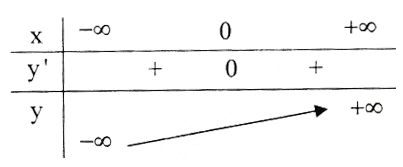
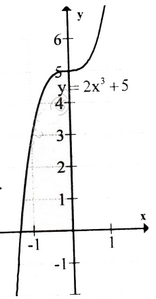
Đồ thị hàm số như hình bên.
Lời giải hay đó!!!
Nhưng không biết người giải nó có hiểu nó không....
(thở dài)
a) Tập xác định : R ; y' =-4x3 + 16x = -4x(x2 - 4);
y' = 0 ⇔ x = 0, x = ±2 .
Bảng biến thiên :
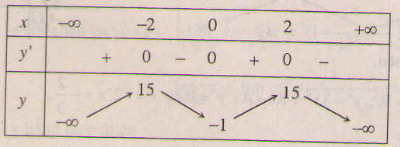
Đồ thị như hình bên.
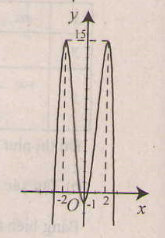
b) Tập xác định : R ; y' =4x3 - 4x = 4x(x2 - 1);
y' = 0 ⇔ x = 0, x = ±1 .
Bảng biến thiên :
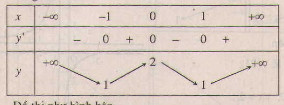
Đồ thị như hình bên.
c) Tập xác định : R ; y' =2x3 + 2x = 2x(x2 + 1); y' = 0 ⇔ x = 0.
Bảng biến thiên :
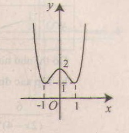
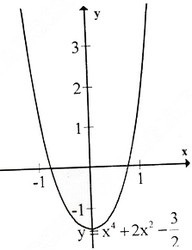
Đồ thị như hình bên.
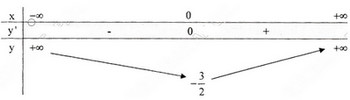
d) Tập xác định : R ; y' = -4x - 4x3 = -4x(1 + x2); y' = 0 ⇔ x = 0.
Bảng biến thiên :
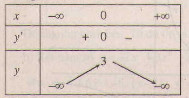
Đồ thị như hình bên.
.
a) (H) có các đường tiệm cận là:
- Tiệm cận ngang y = -1
- Tiệm cận đứng x = -1
hai đường tiềm cận này cắt nhau tại điểm I(-1; -1).
Hình (H') có hai đường tiệm cận cắt nhau tại I'(2;2) nên ta cần phép tịnh tiến theo vector \(\overrightarrow{II'}=\left(2-\left(-1\right);2-\left(-1\right)\right)=\left(3;3\right)\)
b) Hình (H') có phương trình là:
\(y+3=\dfrac{3-\left(x+3\right)}{\left(x+3\right)+1}\) hay là \(y=\dfrac{-4x-12}{x+4}\)
Hình đối xứng với (H') qua gốc tọa độ có phương trình là:
\(-y=\dfrac{-4\left(-x\right)-12}{-x+4}\) hay là: \(y=\dfrac{4x-12}{-x+4}\)
a) Khi a = 0 ta có hàm số: y=−13x3−x2+3x−4y=−13x3−x2+3x−4
- Tập xác định : (-∞, +∞)
- Sự biến thiên: y’= -x2 – 2x + 3
y’=0 ⇔ x = 1, x = -3
Trên các khoảng (-∞, -3) và (1, +∞), y’ < 0 nên hàm số nghịch biến.
Trên khoảng (-3, 1), y’ > 0
_ Cực trị:
Hàm số đạt cực đại tại x = 1, yCD=−73yCD=−73
Hàm số đạt cực tiểu tại x = -3, yCT=−13yCT=−13
_ giới hạn vô cực : limx→+∞=−∞,limx→−∞=+∞limx→+∞=−∞,limx→−∞=+∞
Bảng biến thiên:
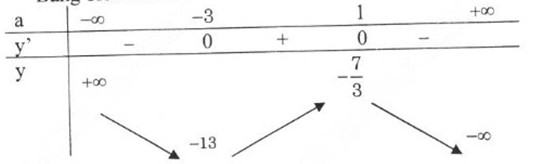
Đồ thị hàm số:
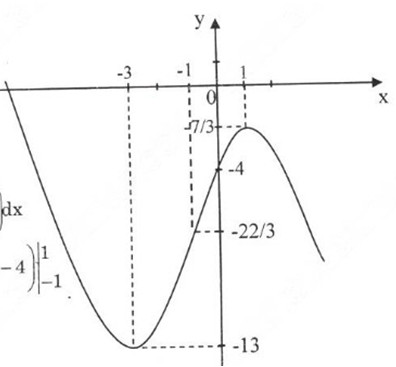
Đồ thị cắt trục tung tại y = -4
Đồ thị cắt trục hoành tại x ≈ 5, 18
b) Hàm số y=−13x3−x2+3x−4y=−13x3−x2+3x−4 đồng biến trên khoảng (-3, 1) nên:
y < y(1) = −73−73 < 0, ∀x ∈ (-1, 1)
Do đó , diện tích cần tính là:
∫1−1(−13x3−x2+3x−4)dx=263
Xem thêm tại: http://loigiaihay.com/cau-2-trang-145-sgk-giai-tich-12-c47a26419.html#ixzz4czxQ4IGx
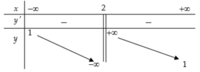
Chọn C
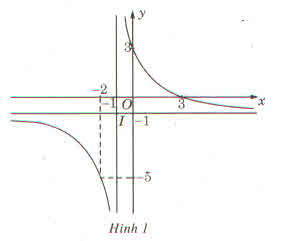
Từ bảng biến thiên của hàm số ta thấy: đồ thị hàm số có tiệm cận ngang là đường thẳng y = 1 nên loại đáp án A và B, hàm số ngịch biến trên mỗi khoảng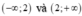
nên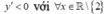 
loại dáp án D, vậy chọn C.