Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) ΔADI và ΔCDL có: góc A = góc C = 90°
AD = CD (hai cạnh hình vuông)
góc D1 = góc D2
cùng phụ với góc CDI
Do đó ΔADI = ΔCDL (g.c.g)
Suy ra DI = DL. Vậy ΔDIL cân
b) Áp dụng hệ thức  là không đổi.
là không đổi.
Nhận xét: Câu a) chỉ là gợi ý để làm câu b). Điều phải chứng minh ở câu b) rất gần với hệ thức 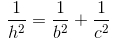
Nếu đề bài không cho vẽ DL ⊥ DK thì ta vẫn phải vẽ đường phụ DL ⊥ DK để có thể vận dụng hệ thức trên.

Xét hai tam giác vuông \(DAE\) và DCG:
\(\widehat{A}=\widehat{C}=90^0\)
\(AD=CD\) (cạnh hình vuông)
\(\widehat{ADE}=\widehat{CDG}\) (cùng phụ \(\widehat{CDE}\))
\(\Rightarrow\Delta DAE=\Delta DCG\left(g.c.g\right)\)
\(\Rightarrow DE=DG\)
\(\Rightarrow\Delta DEG\) cân tại D

đặt góc IAD là D1; góc IDC là D2; góc CDL là D3
a) Ta có D1+D2=90độ
D2+D3=90độ
=>D1=D3
xét 2tam giác vuông IAD và DCL
Có D1=D3(CM trên)
AD=DC(cạnh hình vuông)
=> tam giác IAD=tam giác LCD(góc nhọn-cạnh góc vuông)
=>DL=DI
=> tam giác IDL cân tại D
b) xét tam giác vuông KDL có
DC là đường cao
=> 1/DC^2=(1/DK^2)+(1/DL^2) (1)
Mà DL=DI (2)
mà DC không đổi (3)
Từ (1),(2) và (3) =>DPCM

a) Xét hai tam giác IAD và LCD có:
+DA=DC
+ Góc IAD=Góc LCD=90 (độ)
+ Góc ADI=Góc LDC (cùng phụ với góc IDC)
Hai tam giác đó bằng nhau, nên DI=DL (tam giác IDL câ tại D)
b) Theo câu a) ta có DI=DL
nên: 1/DI.DI+1/DK.DK=1/DL.DL+1/DK.DK
DL và DK là hai cạnh góc vuông của tam giác vuông KDL, đường cao DC, áp dụng hệ thức lượng trong tam giác vuông (nghịch đảo bình phương đường cao, bằng tổng nghịch đảo hai cạnh góc vuông)
ta có: 1/DL.DL+1/DK.DK=1/DC.DC=1/a.a (a: cạnh hình vuông, không đổi)
tick đúng cho mih nhé
Đây là đề bài của e chị ạ, chị làm giúp em nha:
Cho hình vuông ABCD và điểm I ko thay đổi giữa A và B.Tia DI cắt BC tại E, đường thẳng qua D vuông góc với DE cắt BC tại F.
a; Chứng minh tam giác DIF vuông cân

Cho 3 số thực dương a;b;c thỏa mãn : a+ b + c = 1 . CMR
\(\frac{a+1}{a+b+c}+\frac{b+1}{b+ac}+\frac{c+1}{c+ab}\ge9\)Dấu " = " xay ra khi nào

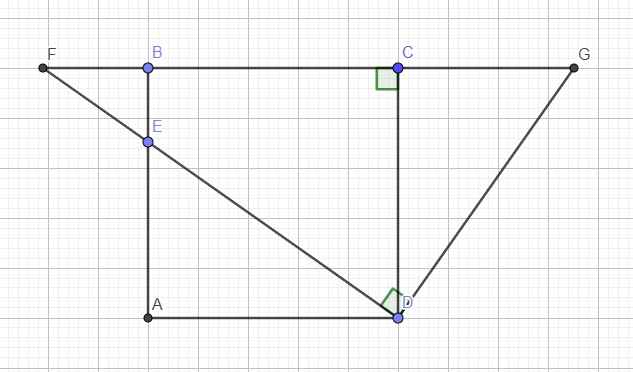
a: \(\widehat{ADE}+\widehat{EDC}=90^0\)
\(\widehat{KDC}+\widehat{EDC}=90^0\)
Do đó: \(\widehat{ADE}=\widehat{KDC}\)
Xét ΔADE vuông tại A và ΔCDK vuông tại C có
DA=DC
\(\widehat{ADE}=\widehat{KDC}\)
Do đó: ΔADE=ΔCDK
=>DE=DK
Xét ΔDEK có
\(\widehat{EDK}=90^0\)
DE=DK
Do đó: ΔDEK vuông cân tại D
b: Xét ΔDFK vuông tại D có DC là đường cao
nên \(\dfrac{1}{DK^2}+\dfrac{1}{DF^2}=\dfrac{1}{DC^2}\)
=>\(\dfrac{1}{DE^2}+\dfrac{1}{DF^2}=\dfrac{1}{DC^2}\) không đổi