Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C D F E #Hinh_anh_chi_mang_tinh_chat_minh_hoa
Vi tu giac ABCD co ^A = ^C = 90o => ^B + ^D = 180o
Kẻ phân giác DF , BE
Xét \(\Delta BEC\)vuông tại C nên \(\widehat{CBE}+\widehat{CEB}=90^o\)
\(\Rightarrow2\left(\widehat{CBE}+\widehat{CEB}\right)=180^o\)
\(\Rightarrow\widehat{CBA}+2\widehat{CEB}=180^o\)
Tuong tu \(\widehat{CDA}+2\widehat{AFD}=180^o\)
\(\Rightarrow\left(\widehat{CBA}+\widehat{CDA}\right)+2\left(\widehat{CEB}+\widehat{AFD}\right)=360^o\)
\(\Leftrightarrow180^o+2\left(\widehat{CEB}+\widehat{AFD}\right)=360^o\)
\(\Leftrightarrow\widehat{CEB}+\widehat{AFD}=90^o\)
\(\Rightarrow\widehat{CBE}=\widehat{AFD}\)(Cùng phụ \(\widehat{CEB}\))
\(\Rightarrow\widehat{ABE}=\widehat{AFD}\)(Phan giac)
\(\Rightarrow FD//\left(h\right)\equiv BE\left(dpcm\right)\)

a. Xét tam giác HCD cóHN=DN;HM=CM
=> MN là đường trung bình của tam giác HCD => MN//DC
=> DNMC là hình thang
b. Ta có MN là đường trung bình của tam giác HCD => MN=1/2CD
Mà AB=1/2CD => AB =MN
Do MN//CD và AB//CD => AB//MN
Xét tứ giác ABMN có AB//MN; AB=MN
=> ABMN là hình bình hành
c.Ta có MN//CD mà CD vg AD
=> MN vg AD
Xét tam giác ADM có DH và MN là 2 đường cao của tam giác
Mà chúng cắt nhau tại N nên N là trực tâm của tam giác ADM
=> AN là đường cao của tam giác ADM
=> AN vg DM
Do ABMN là hình bình hành nên AN//BM
=> BM vg DM => BMD =90*
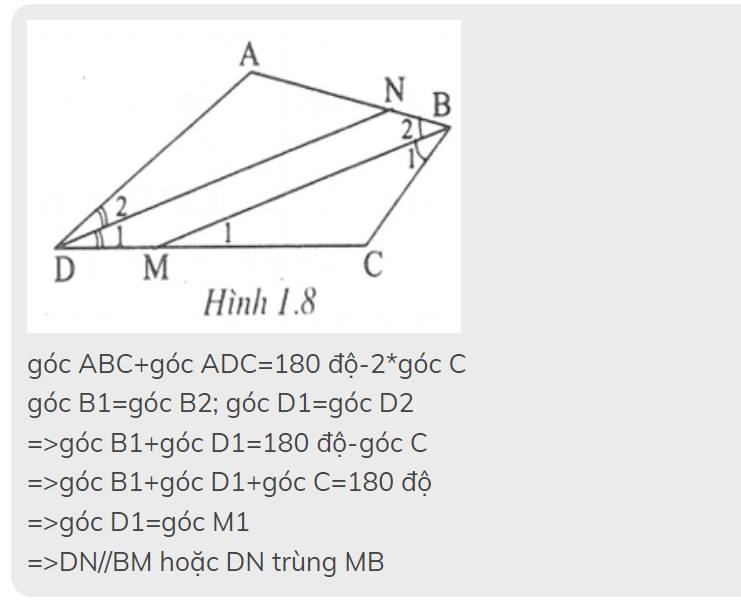
TH1: ABCD không phải là hình thoi hoặc hình vuông
Gọi BM,DN lần lượt là phân giác của \(\widehat{ABC};\widehat{ADC}\)
Xét tứ giác ABCD có
\(\widehat{BAD}+\widehat{ABC}+\widehat{BCD}+\widehat{ADC}=360^0\)
=>\(2\cdot\left(\widehat{NBM}+\widehat{NDM}\right)=360^0-\widehat{A}-\widehat{C}=360^0-2\cdot\widehat{C}\)
=>\(\widehat{NBM}+\widehat{NDM}=180^0-\widehat{C}\)(1)
Xét ΔCMB có
\(\widehat{C}+\widehat{CMB}+\widehat{CBM}=180^0\)
=>\(\widehat{CMB}+\widehat{NBM}=180^0-\widehat{C}\)(2)
Từ (1) và (2) suy ra \(\widehat{NDM}=\widehat{CMB}\)
mà hai góc này ở vị trí đồng vị
nên BM//DN (ĐPCM)
TH2: ABCD là hình thoi hoặc hình vuông
ABCD là hình thoi
=>BD là tia phân giác của \(\widehat{ABC}\) và DB là tia phân giác của \(\widehat{ADC}\)
=>Các đường phân giác của góc B và góc D trùng nhau