Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

TH1: ABCD không phải là hình thoi hoặc hình vuông
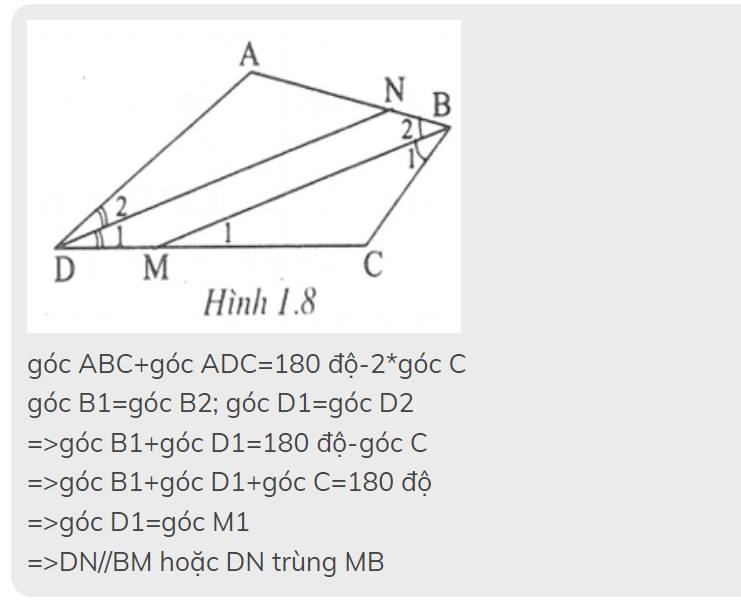
Gọi BM,DN lần lượt là phân giác của \(\widehat{ABC};\widehat{ADC}\)
Xét tứ giác ABCD có
\(\widehat{BAD}+\widehat{ABC}+\widehat{BCD}+\widehat{ADC}=360^0\)
=>\(2\cdot\left(\widehat{NBM}+\widehat{NDM}\right)=360^0-\widehat{A}-\widehat{C}=360^0-2\cdot\widehat{C}\)
=>\(\widehat{NBM}+\widehat{NDM}=180^0-\widehat{C}\)(1)
Xét ΔCMB có
\(\widehat{C}+\widehat{CMB}+\widehat{CBM}=180^0\)
=>\(\widehat{CMB}+\widehat{NBM}=180^0-\widehat{C}\)(2)
Từ (1) và (2) suy ra \(\widehat{NDM}=\widehat{CMB}\)
mà hai góc này ở vị trí đồng vị
nên BM//DN (ĐPCM)
TH2: ABCD là hình thoi hoặc hình vuông
ABCD là hình thoi
=>BD là tia phân giác của \(\widehat{ABC}\) và DB là tia phân giác của \(\widehat{ADC}\)
=>Các đường phân giác của góc B và góc D trùng nhau

https://olm.vn/hoi-dap/detail/82663575347.html
Tham khảo ở link này (mình gửi cho)
Còn cm trùng nhau là trường hợp đặc biệt khi \(\widehat{B}=\widehat{D}\)
Phân giác góc B cắt DC tại E
Phân giác góc D cắt AB tại I
Phân giác góc D trùng góc B do D1 = B2 ( slt )
D2 = B1 ( slt )

a) Gọi E, F lần lượt là giao điểm của AM và CD, BN và CD
Ta có : AB//CD (gt) => E = A1 (so le trong)
Mà A1 =A2 (gt)
Nên A2 = E
Xét ΔADE cân tại D, có DM là p/giác nên DM đồng thời là trung tuyến
=>AM= EM
Chứng minh tương tự, ta được :
BN = FN
Xét hình thang ABEF có : AM=BN(cm trên)
BN=FN(cm trên)
Do đó MN là đường TB của HÌNH thang ABEF
=> MN= \(\frac{EF+AB}{2}\)
MN//AB//EF Vậy MN// CD(đpcm)
b)Do ED= AD; BC=FC
Mà ED + DC + CF = EF
Nên AD + DC + BC = EF
Lại có MN \(\frac{EF+AB}{2}\)(CM trên)
Suy ra MN= \(\frac{AD+DC+BC+AB}{2}\)\(=\frac{a+b+c+d}{2}\)