



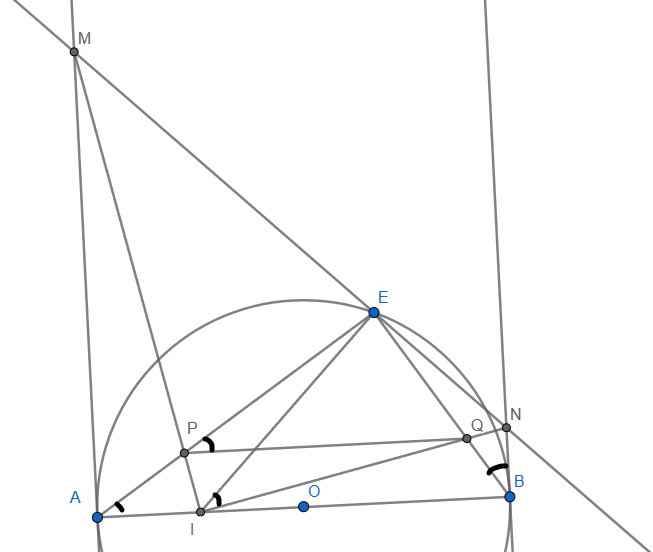
 Mình gửi hình nhé
Mình gửi hình nhé
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




 Mình gửi hình nhé
Mình gửi hình nhé

a: Xet (O) có
CE,CA là các tiếp tuyến
nên CE=CA và OC là phân giác của góc EOA(1)
mà OE=OA
nên OC là trung trực của AE
=>OC vuông góc với AE
Xét (O) có
DE,DB là các tiếp tuyến
nen DE=DB và OD là phân giác của góc EOB(2)
mà OE=OB
nên OD là trung trực của BE
=>OD vuông góc với BE
CE+ED=CD
=>CD=CA+BD
b: Từ (1), (2) suy ra góc COD=1/2*180=90 độ
Xét tứ giác EIOK co
góc EIO=góc EKO=góc IOK=90 độ
nên EIOK là hình chữ nhật

Em tham khảo tại link dưới đây nhé.
Câu hỏi của My Trấn - Toán lớp 9 - Học toán với OnlineMath
Với câu c, khi đã có IK // AD thì vận dụng Ta let ta có ngay \(\frac{IC}{AD}=\frac{IK}{AD}\Rightarrow IC=IK\)

A B E F x y M K O
a)\(\hept{\begin{cases}Ax⊥AB\\By⊥AB\end{cases}}\)=> Ax // By.\(\Delta KFB\)có EA // FB nên\(\frac{KF}{KA}=\frac{BF}{AE}\)(hệ quả định lí Ta-lét) mà EA = EM ; FM = FB (tính chất của 2 tiếp tuyến)
\(\Rightarrow\Delta AEF\)có\(\frac{KF}{KA}=\frac{MF}{ME}\)nên MK // AE (định lí Ta-lét đảo) mà\(AE⊥AB\Rightarrow MK⊥AB\)
b)\(\widehat{EOM}=\frac{\widehat{AOM}}{2};\widehat{FOM}=\frac{\widehat{MOB}}{2}\)(tính chất 2 tiếp tuyến) mà\(\widehat{EOM}+\widehat{FOM}=180^0\)(kề bù)
\(\Rightarrow\widehat{EOF}=\widehat{EOM}+\widehat{FOM}=\frac{180^0}{2}=90^0\)
\(\Rightarrow\Delta EOF\)vuông tại O có OE + OF > EF (bđt tam giác) ; OE + OF < 2EF (vì OE,OF < EF)
\(\Rightarrow1< \frac{OE+OF}{EF}< 2\Rightarrow2< \frac{P_{EOF}}{EF}< 3\Rightarrow\frac{1}{3}< \frac{EF}{P_{EOF}}< \frac{1}{2}\)(1)
Hình thang AEFB (AE // FB) có diện tích là :\(\frac{\left(AE+FB\right).AB}{2}=\frac{\left(EM+FM\right).2R}{2}=EF.R\)
SAEO = SMEO vì có đáy OA = OM ; đường cao AE = ME\(\Rightarrow S_{MEO}=\frac{1}{2}S_{AEMO}\)
SFOM = SFOB vì có đáy FM = FB ; đường cao OM = OB\(\Rightarrow S_{FOM}=\frac{1}{2}S_{MFBO}\)
\(\Rightarrow S_{EOF}=\frac{1}{2}\left(S_{AEMO}+S_{MFBO}\right)=\frac{EF.R}{2}\).Từ tâm đường tròn nội tiếp I của\(\Delta EOF\)kẻ các đường vuông góc với OE,OF,EF thì\(S_{EOF}=S_{EIF}+S_{EIO}+S_{OIF}\)\(\Leftrightarrow\frac{EF.R}{2}=\frac{EF.r+EO.r+OF.r}{2}\)
\(\Rightarrow EF.R=P_{EOF}.r\Rightarrow\frac{r}{R}=\frac{EF}{P_{EOF}}\)(2).Thay (2) vào (1) ta có đpcm.