

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Giải toán bằng cách lập phương trình:
Gọi vận tốc ca nô khi nước lặng là: \(x\) km/h ( \(x\) > 0)
Vận tốc ca nô khi xuôi dòng là: \(x\) + 5 ( km/h)
Thời gian ca nô xuôi dòng là: \(\dfrac{60}{x+5}\) (giờ)
Vận tốc ca nô khi ngược dòng là: \(x\) -5 ( km/h)
Thời gian ca nô ngược dòng là: \(\dfrac{60}{x-5}\) ( giờ)
Theo bài ra ta có phương trình:
\(\dfrac{60}{x+5}+\dfrac{60}{x-5}\) = 5 = \(\dfrac{60}{12}\)
⇒ \(\dfrac{1}{x+5}\) + \(\dfrac{1}{x-5}\) = \(\dfrac{1}{12}\)
⇒ 12 \(\times\) ( \(x+5+x-5\)) = (\(x\) + 5)(\(x-5\))
⇒ 12 \(\times\) 2\(x\) = \(x^2\) - 25
\(x^2\) - 25 - 24\(x\) = 0 ⇒ \(x^2\) - 24\(x\) - 25 = 0
ta có a - b + c = 1 - ( -24) - 25 = 0 ⇒ \(x\) = -1 ( loại); \(x\)= 25 ( thỏa mãn)
Vậy vận tốc ca nô khi nước lặng là 25 km/h

Gọi vận tốc thực của canô là x (km/h) (x > 3)
Gọi vận tốc xuôi dòng là : x + 3 (km/h)
Gọi vận tốc khi ngược dòng là : x – 3 (km/h)

Do kể từ lúc khởi hành đến khi về tới bến A hết tất cả 6 h nên ta có:
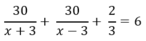
⇔ 30.3 (x- 3) + 30.3. (x+ 3) + 2(x+ 3). (x – 3) = 6.3.(x+3).(x – 3)
⇔ 90.(x – 3) + 90(x+ 3)+ 2(x2 – 9) = 18 (x2 -9)
⇔ 90x – 270+ 90x + 270 + 2x2 – 18 = 18x2 – 162
⇔ 180x + 2x2 – 18 = 18x2 – 162
⇔ 16x2 – 180x -144= 0
⇔ 4x2 –45x – 36 = 0
Có a=4; b= - 45, c= - 36
∆= ( -45)2 – 4.4.(- 36)= 2601 > 0
Phương trình đã cho có hai nghiệm là:
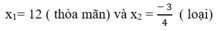
Vậy vận tốc của canô trong nước yên lặng là 12km/h.

Gọi vận tốc thực của canô là x (km/h) (x > 3)
Gọi vận tốc xuôi dòng là : x + 3 (km/h)
Gọi vận tốc khi ngược dòng là : x – 3 (km/h)

Do kể từ lúc khởi hành đến khi về tới bến A hết tất cả 6 h nên ta có:
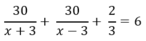
⇔ 30.3 (x- 3) + 30.3. (x+ 3) + 2(x+ 3). (x – 3) = 6.3.(x+3).(x – 3)
⇔ 90. ( x − 3 ) + 90 ( x + 3 ) + 2 x 2 − 9 = 18 x 2 − 9 ⇔ 90 x − 270 + 90 x + 270 + 2 x 2 − 18 = 18 x 2 − 162 ⇔ 180 x + 2 x 2 − 18 = 18 x 2 − 162 ⇔ 16 x 2 − 180 x − 144 = 0 ⇔ 4 x 2 − 45 x − 36 = 0
Có a=4; b= - 45, c= - 36
∆ = ( - 45 ) 2 – 4 . 4 . ( - 36 ) = 2601 > 0
Phương trình đã cho có hai nghiệm là:
![]()
Vậy vận tốc của canô trong nước yên lặng là 12km/h.

*Gọi vận tốc riêng của thuyền là x (km/h) (1<x < 60)
Vận tốc khi xuồng xuôi dòng là: x + 1 (km/h)
Vận tốc khi xuồng ngược dòng là: x - 1(km/h)
*Thời gian xuồng xuôi dòng từ A --> B là: 60/(x + 1) (h)
Thời gian xuồng xuôi dòng đến bến C là: 25/(x - 1) (h)
30 phút = 1/2 (h)
*Vì thời gian kể từ lúc đi đến lúc quay trở lại đến bến C hết tất cả là 8 giờ nên ta có PT:
60/(x + 1) + 25/(x - 1) + 1/2 = 8
=> 60.2.(x - 1) + 25.2(x + 1) + (x - 1)(x + 1) = 8.2(x - 1)(x + 1)
<=> 120x - 120 + 50x + 50 + x^2 - 1 = 16x^2 - 16
<=> 15x^2 - 170x + 55 = 0
delta' = (- 85)^2 - 55.15 = 6400 = 80^2 > 0
=> PT có 2 nghiệm pb:
x1 = (85 - 80)/15 = 1/3 (loại)
x2 = (85 + 80)/15 = 11 (thỏa mãn điều kiện bài ra)
Vậy vận tốc xuồng máy khi nước yên lặng là 11km/h

Gọi vận tốc thực của canô là x (km/h), x > 3.
Gọi vận tốc khi đi xuôi dòng là: x + 3 (km/h)
Gọi vận tốc khi ngược dòng là: x - 3 (km/h)
Thời gian xuôi dòng là: \(\dfrac{30}{x+3}\)(giờ)
Thời gian ngược dòng là: \(\dfrac{30}{x-3}\)(giờ)
Nghỉ lại 40 phút hay \(\dfrac{2}{3}\) giờ ở B.
Theo đầu bài ta có phương trình : \(\dfrac{30}{x+3}+\dfrac{30}{x+3}+\dfrac{2}{3}=6\)
Giải phương trình:
16(x + 3)(x - 3) = 90(x + 3 + x - 3) hay: 4x2 - 45x - 36 = 0
\(\Delta\)= 2025 + 576 = 2601, \(\sqrt{\Delta}\) = 51
x1 = 12, x2 = \(\dfrac{-3}{4}\)(loại)
=> Vận tốc của canô trong nước yên lặng là 12 km/h.
Phương trình Giang viết có một chút sai sót nhỏ. Lần sau cần cẩn thận hơn em nhé.
Phương trình đúng phải là: \(\dfrac{30}{x-3}+\dfrac{30}{x+3}+\dfrac{2}{3}=6.\)

C1: Một canô ngược dòng từ bến A đến bến B với vận tốc 20 km/h, sau đó lại xuôi từ bến B trở về bến A. Thời gian canô ngược dòng từ A đến B nhiều hơn thời gian canô xuôi dòng từ B trở về A là 2 giờ 40 phút. Tính khoảng cách giữa hai bến A và B. Biết vận tốc dòng nước là 5 km/h, vận tốc riêng của canô lúc xuôi dòng và lúc ngược dòng bằng nhau.
Giải: 2 giờ 40 phút = \(\dfrac{8}{3}\) giờ.
Vận tốc thực của cano là: \(20+5=25\left(km/h\right).\)
Vận tốc cano đi xuôi dòng là: \(25+5=30\left(km/h\right).\)
Gọi thời gian cano đi xuôi dòng là: \(x\left(h\right);x>0.\)
\(\Rightarrow\) Thời gian cano đi ngược dòng là: \(x+\dfrac{8}{3}\left(h\right).\)
Quãng đường cano đi xuôi dòng là: \(30x\left(km\right).\)
Quãng đường cano đi ngược dòng là:
\(20\left(x+\dfrac{8}{3}\right)=20x+\dfrac{160}{3}\left(km\right).\)
Vì cano đi xuôi và ngược đều cùng trên 1 quãng đường nên ta có phương trình sau:
\(30x=20x+\dfrac{160}{3}.\\ \Leftrightarrow10x-\dfrac{160}{3}=0.\\ \Leftrightarrow x=\dfrac{16}{3}\left(TM\right).\)
\(\Rightarrow\) Khoảng cách giữa hai bến A và B là: \(30.\dfrac{16}{3}=160\left(km\right).\)