
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Nếu nghĩ kĩ thì thấy bài này cũng đơn giản thôi.Thử xem cách giải của mk nè:
Giải: Ta có: A=\(\frac{17^{18}+1}{17^{19}+1}\) B=\(\frac{17^{17}+1}{17^{18}+1}\)
17A=\(\frac{17^{19}+17}{17^{19}+1}\) 17B=\(\frac{17^{18}+17}{17^{18}+1}\)
17A=\(\frac{\left(17^{19}+1\right)+16}{17^{19}+1}\) 17B=\(\frac{\left(17^{18}+1\right)+16}{17^{18}+1}\)
17A=\(\frac{17^{19}+1}{17^{19}+1}+\frac{16}{17^{19}+1}\) 17B=\(\frac{17^{18}+1}{17^{18}+1}+\frac{16}{17^{18}+1}\)
17A=\(1+\frac{16}{17^{19}+1}\) 17B= \(1+\frac{16}{17^{18}+1}\)
Lại có: 1719+1>1718+1
Suy ra:\(\frac{16}{17^{19}+1}< \frac{16}{17^{18}+1}\)
17A<17B
A<B
Vậy A<B
\(\text{Ta có:}\frac{17^{18}+1}{17^{19}+1}\)
\(\Rightarrow17A=\frac{17^{19}+1+16}{17^{19}+1}\)
\(\Rightarrow17A=1+\frac{16}{17^{19}+1}\)
\(B=\frac{17^{17}+1}{17^{18}+1}\)
\(\Rightarrow17B=\frac{17^{18}+1+16}{17^{18}+1}\)
\(\Rightarrow17B=1+\frac{16}{17^{18}+1}\)
\(\text{Vì }\frac{16}{17^{19}+1}< \frac{16}{17^{18}+1}\)
\(\Rightarrow17A< 17B\)
\(\Rightarrow A< B\)

Ta có: \(A=\frac{17^{18}+1}{17^{19}+1}<1\)
\(A=\frac{17^{18}+1}{17^{19}+1}<\frac{17^{18}+1+16}{17^{19}+1+16}=\frac{17^{18}+17}{17^{19}+17}=\frac{17\left(17^{17}+1\right)}{17\left(17^{18}+1\right)}=B\)
=> A<B
Để so sánh A =1718+1/1719+1 và B=1717+1/1718+1
=>Ta xét bài toán phụ sau
a/b<1 thì a/b<a+/b+m
vì a/b<1=>a<b mà m thuộc N*
=>a.m<b.m=>ab+am<ab+bm
a/b=a.(b+m0/b.(b+m)/b(b+m=ab+am/b(b+m)<ab+bm/b(b+m)
Vì b(b+m)>0=>a/b<ab+bm/b(b+m)=b(a+m)/b(b+m)=a+m/b+m
=>.a/b<a+m/b+m(1)
vì 1718+ 1 < 1719+1
=>A<1
(1)=>1718+1/1719+1<1718+1+16/1719+1+16
<=>A<1717+17/1719+17=17(1717+1)/1791718+1)
<=>A<1717+1/1718+1=B
<=>A<B
Vậy...


1) Phân tích A ra :
A= 1717.17+$\frac{1}{17^{18}.17}$11718.17 +1 So sánh với B ta có: A có 1718>1717 của B nhưng B lại có 1/1718>1/1719.
Mà 1718>1/1718 nên suy ra A>B

Giải
\(A=\frac{17^{18}+1}{17^{19}+1}\Leftrightarrow17A=\frac{17\left(17^{18}+1\right)}{17^{19}+1}\)
\(\Leftrightarrow17A=\frac{17^{19}+17}{17^{19}+1}\)
\(\Leftrightarrow17A=\frac{17^{19}+1+16}{17^{19}+1}\)
\(\Leftrightarrow17A=\frac{17^{19}+1}{17^{19}+1}+\frac{16}{17^{19}+1}\)
\(\Leftrightarrow17A=1+\frac{16}{17^{19}+1}\left(1\right)\)
\(B=\frac{17^{17}+1}{17^{18}+1}\Leftrightarrow17B=\frac{17\left(17^{17}+1\right)}{17^{18}+1}\)
\(\Leftrightarrow17B=\frac{17^{18}+17}{17^{18}+1}\)
\(\Leftrightarrow17B=\frac{17^{18}+1+16}{17^{18}+1}\)
\(\Leftrightarrow17B=\frac{17^{18}+1}{17^{18}+1}+\frac{16}{17^{18}+1}\)
\(\Leftrightarrow17B=1+\frac{16}{17^{18}+1}\left(2\right)\)
Từ (1) và (2) suy ra 17A < 17B
Suy ra A < B

Ta có:
\(A=\frac{17^{18}+1}{17^{19}+1}\)
\(17A=\frac{17\left(17^{18}+1\right)}{17^{19}+1}=\frac{17^{19}+17}{17^{19}+1}\)
\(17A=\frac{(17^{19}+1)+16}{(17^{19}+1)}=1+\frac{16}{17^{19}+1}\) (1)
\(B=\frac{17^{17}+1}{17^{18}+1}\)
\(17B=\frac{17\left(17^{17}+1\right)}{17^{18}+1}=\frac{17^{18}+17}{17^{18}+1}\)
\(17B=\frac{(17^{18}+1)+16}{(17^{18}+1)}=1+\frac{16}{17^{18}+1}\) (2)
Từ (1) và (2) => \(1+\frac{16}{17^{19}+1}< 1+\frac{16}{17^{18}+1}\)
=>\(17A< 17B\)
Hay \(A< B\)
Vậy \(A< B\)
Ta có công thức :
\(\frac{a}{b}< \frac{a+c}{b+c}\)\(\left(\frac{a}{b}< 1;a,b,c\inℕ^∗\right)\)
Áp dụng vào ta có :
\(A=\frac{17^{18}+1}{17^{19}+1}< \frac{17^{18}+1+16}{17^{19}+1+16}=\frac{17^{18}+17}{17^{19}+17}=\frac{17\left(17^{17}+1\right)}{17\left(17^{18}+1\right)}=\frac{17^{17}+1}{17^{18}+1}=B\)
Vậy \(A< B\)
Chúc bạn học tốt ~
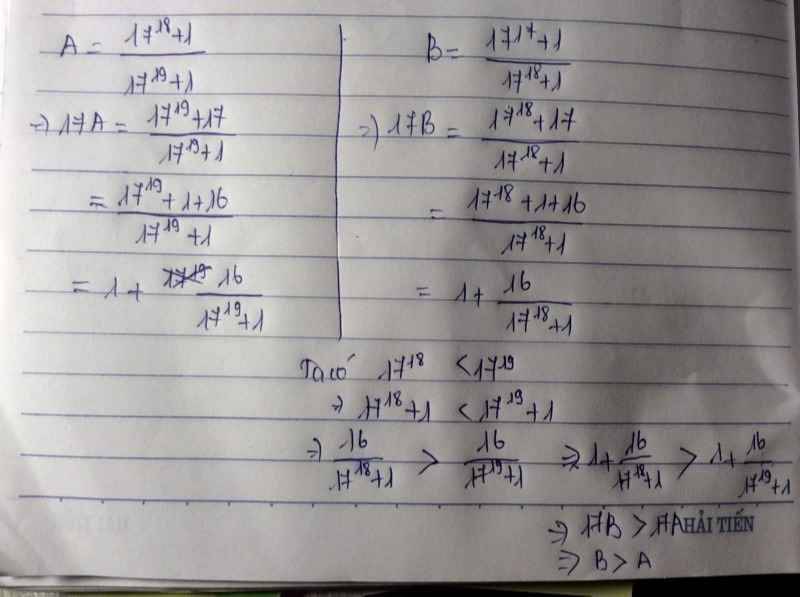
Ta có công thức :
\(\frac{a}{b}< \frac{a+c}{b+c}\left(\frac{a}{b}< 1;a,b,c\inℕ^∗\right)\)
Áp dụng vào ta có :
\(A=\frac{17^{18}+1}{17^{19}+1}< \frac{17^{18}+1+16}{17^{19}+1+16}\)
\(=\frac{17^{18}+17}{17^{19}+17}\)
\(=\frac{17\left(17^{17}+1\right)}{17\left(17^{18}+1\right)}\)
\(\Leftrightarrow\frac{17^{17}+1}{17^{18}+1}\)'
\(\Rightarrow=B\)
Vậy \(A< B\)