Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài này có rất nhiều cách lm nhé!
Ta có : A = \(\dfrac{17^{18}+1}{17^{19}+1}\) => 17A = \(\dfrac{17^{19}+17}{17^{19}+1}\) = \(1+\dfrac{16}{17^{19}+1}\)
B = \(\dfrac{17^{17}+1}{17^{18}+1}\) => 17B = \(\dfrac{17^{18}+17}{17^{18}+1}\) = \(1+\dfrac{16}{17^{18}+1}\)
Vì \(\dfrac{16}{17^{19}+1}\) < \(\dfrac{16}{17^{18}+1}\) ( vì 1719 +1 > 1716+1 )
=> \(1+\dfrac{16}{17^{19}+1}\) < \(1+\dfrac{16}{17^{18}+1}\)
=> 17A < 17B
=> A < B ( vì 17 > 0)
Ta có :
\(A=\dfrac{17^{18}+1}{17^{19}+1}\)
17A= \(17\times\dfrac{17^{18}+1}{17^{19}+1}\)
\(17A=\dfrac{17^{19}+17}{17^{19}+1}\)
\(17A=\dfrac{\left(17^{19}+1\right)+16}{17^{19}+1}\)
\(17A=\dfrac{17^{19}+1}{17^{19}+1}+\dfrac{16}{17^{19}+1}\)
\(17A=1+\dfrac{16}{17^{19}+1}\)
Lại có :
\(B=\dfrac{17^{17}+1}{17^{18}+1}\)
\(17B=17\times\dfrac{17^{17}+1}{17^{18}+1}\)
\(17B=\dfrac{17^{18}+17}{17^{18}+1}\)
\(17B=\dfrac{\left(17^{18}+1\right)+16}{17^{18}+1}\)
\(17B=\dfrac{17^{18}+1}{17^{18}+1}+\dfrac{16}{17^{18}+1}\)
\(17B=1+\dfrac{16}{17^{18}+1}\)
Mà : \(\dfrac{16}{17^{19}+1}< \dfrac{16}{17^{18}+1}\)
\(\Rightarrow1+\dfrac{16}{17^{19}+1}< 1+\dfrac{16}{17^{18}+1}\)
⇒ A < B
Vậy A < B

Ta có:
\(A=\frac{17^{18}+1}{17^{19}+1}\)
\(17A=\frac{17\left(17^{18}+1\right)}{17^{19}+1}=\frac{17^{19}+17}{17^{19}+1}\)
\(17A=\frac{(17^{19}+1)+16}{(17^{19}+1)}=1+\frac{16}{17^{19}+1}\) (1)
\(B=\frac{17^{17}+1}{17^{18}+1}\)
\(17B=\frac{17\left(17^{17}+1\right)}{17^{18}+1}=\frac{17^{18}+17}{17^{18}+1}\)
\(17B=\frac{(17^{18}+1)+16}{(17^{18}+1)}=1+\frac{16}{17^{18}+1}\) (2)
Từ (1) và (2) => \(1+\frac{16}{17^{19}+1}< 1+\frac{16}{17^{18}+1}\)
=>\(17A< 17B\)
Hay \(A< B\)
Vậy \(A< B\)
Ta có công thức :
\(\frac{a}{b}< \frac{a+c}{b+c}\)\(\left(\frac{a}{b}< 1;a,b,c\inℕ^∗\right)\)
Áp dụng vào ta có :
\(A=\frac{17^{18}+1}{17^{19}+1}< \frac{17^{18}+1+16}{17^{19}+1+16}=\frac{17^{18}+17}{17^{19}+17}=\frac{17\left(17^{17}+1\right)}{17\left(17^{18}+1\right)}=\frac{17^{17}+1}{17^{18}+1}=B\)
Vậy \(A< B\)
Chúc bạn học tốt ~

áp dụng tính chất \(\frac{a}{b}< 1\Rightarrow\frac{a+m}{b+m}< 1\left(m\in N\right)\)
Ta có: \(A=\frac{17^{18}-1}{17^{20}-1}< \frac{17^{18}-1-16}{17^{20}-1-16}\)\(=\frac{17^{18}-17}{17^{20}-17}=\frac{17.\left(17^{17}-1\right)}{17.\left(17^{19}-1\right)}\)\(=\frac{17^{17}-1}{17^{19}-1}\)
\(\Rightarrow A< B\)
\(A=\frac{17^{18}-1}{17^{20}-1}\Rightarrow17^2A=\frac{17^{18}-1}{17^{18}-\frac{1}{17^2}}=1-\frac{1-\frac{1}{17^2}}{17^{18}-\frac{1}{17^2}}\left(1\right)\)
\(B=\frac{17^{17}-1}{17^{19}-1}\Rightarrow17^2B=\frac{17^{17}-1}{17^{17}-\frac{1}{17^2}}=1-\frac{1-\frac{1}{17^2}}{17^{17}-\frac{1}{17^2}}\left(2\right)\)
\(\frac{1-\frac{1}{17^2}}{17^{18}-\frac{1}{17^2}}< \frac{1-\frac{1}{17^2}}{17^{17}-\frac{1}{17^2}}\Rightarrow1-\frac{1-\frac{1}{17^2}}{17^{18}-\frac{1}{17^2}}>1-\frac{1-\frac{1}{17^2}}{17^{17}-\frac{1}{17^2}}\left(3\right)\)
Từ \(\left(1\right);\left(2\right)\&\left(3\right)\Rightarrow17^2A>17^2B\Leftrightarrow A>B.\)

Bài 1:
Ta thấy A < 1
=> A = \(\frac{17^{18}+1}{17^{19}+1}< \frac{17^{18}+1+16}{17^{19}+1+16}=\frac{17^{18}+17}{17^{19}+17}=\frac{17\left(17^{17}+1\right)}{17\left(17^{18}+1\right)}=\frac{17^{17}+1}{17^{18}+1}=B\)
Vậy A < B
Bài 2:
Ta thấy C < 1
=> C = \(\frac{98^{99}+1}{98^{89}+1}< \frac{98^{99}+1+97}{98^{89}+1+97}=\frac{98^{99}+98}{98^{89}+98}=\frac{98\left(98^{98}+1\right)}{98\left(98^{88}+1\right)}=\frac{98^{98}+1}{98^{88}+1}=D\)
Vậy C < D

\(A=\frac{17^{18}+1}{17^{19}+1}< \frac{17^{18}+1+16}{17^{19}+1+16}\)
\(A=\frac{17^{18}+1}{17^{19}+1}< \frac{17^{18}+17}{17^{19}+17}\)
\(A=\frac{17^{18}+1}{17^{19}+1}< \frac{17^{17}+1}{17^{18}+1}=B\)
=> A < B

\(A=\frac{17^{18}+1}{17^{19}+1}\) <=> \(17A=\frac{17^{19}+17}{17^{19}+1}=\frac{17^{19}+1+16}{17^{19}+1}=1+\frac{16}{17^{19}+1}\)
\(B=\frac{17^{17}+1}{17^{18}+1}\)<=> \(17B=\frac{17^{18}+17}{17^{18}+1}=\frac{17^{18}+1+16}{17^{18}+1}=1+\frac{16}{17^{18}+1}\)
Nhận thấy: 1719+1 > 1718+1 => \(\frac{16}{17^{18}+1}>\frac{16}{17^{19}+1}\)
=> 17B > 17A
=> B > A
Tham khảo :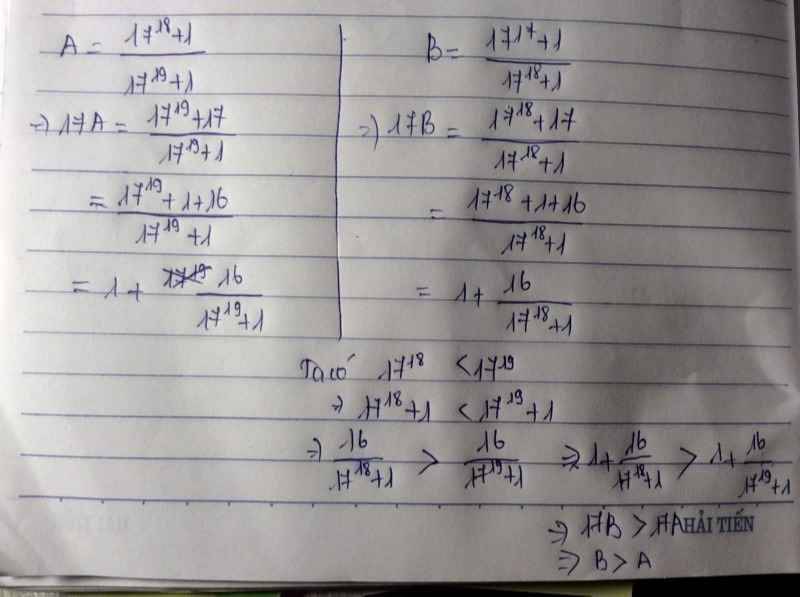
cảm ơn chị nhiều.