Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

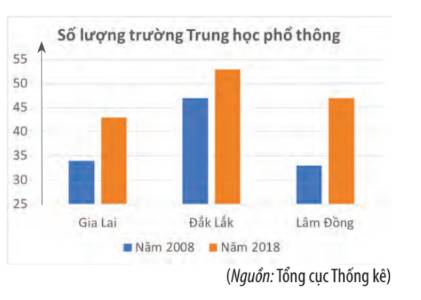
Nhìn vào biểu đồ ta thấy số lượng trường THPT của các tỉnh năm 2018 đều lớn hơn so với năm 2008 nên khẳng định ở câu a) là đúng.
Số lượng trường THPT ở Gia Lai năm 2008 là gần 35 trường, nhưng số lượng trường năm 2018 lại nhỏ hơn 45 trường do đó khẳng định ở câu b) là sai.

a)
Tỉnh Thái Bình:
Số trung bình \(\overline x = \frac{{1061,9 + 1061,9 + 1053,6 + 942,6 + 1030,4}}{5} = 1030,08\)
Phương sai \({S^2} = \frac{1}{5}\left( {1061,{9^2} + 1061,{9^2} + 1053,{6^2} + 942,{6^2} + 1030,{4^2}} \right) - 1030,{08^2} = 2046,2\)
=> Độ lệch chuẩn \(S = \sqrt {{S^2}} \approx 45,2\)
+) Khoảng biến thiên \(R = 1061,9 - 942,6 = 119,3\)
Tỉnh Hậu Giang:
Số trung bình \(\overline x = \frac{{1204,6 + 1293,1 + 1231,0 + 1261,0 + 1246,1}}{5} = 1247,16\)
Phương sai \({S^2} = \frac{1}{6}\left( {1204,{6^2} + 1293,{1^2} + 1231,{0^2} + 1261,{0^2} + 1246,{1^2}} \right) - 1247,{16^2} = 875,13\)
=> Độ lệch chuẩn \(S = \sqrt {{S^2}} \approx 29,6\)
+) Khoảng biến thiên \(R = 1293,1 - 1204,6 = 88,5\)
b)
So sánh khoảng biến thiên và độ lệch chuẩn ta đều thấy tỉnh Hậu Giang có sản lượng lúa ổn định hơn.

Nhìn vào biểu đồ ta thấy giá trị sản phẩm trung bình thu được trên một hecta mặt nước nuôi trồng thủy sản đều cao hơn trên một hecta đất trồng trọt nên khẳng định ở câu a) là đúng.
Dễ thấy giá trị sản phẩm trung bình thu được trên một hecta mặt nước nuôi trồng thủy sản (hoặc đất trồng trọt) đều có xu hướng tăng từ năm 2014 đến năm 2018. Do đó, khẳng định ở câu b2,3) là đúng.
Từ năm 2014 đến năm 2018, giá trị sản phẩm trung bình thu được trên một hecta đất trồng trọt tăng từ khoảng 80 đến 95, trong khi trên một hecta mặt nước nuôi trồng thủy sản là từ gần 180 đến 225, gấp cao gấp khoảng 2,3 lần. Do đó khẳng định ở câu c) là sai.

a) - Số dân tỉnh đó sau 1 năm là: \(800 + 800.r\% = 800.\left( {1 + r\% } \right)\)
- Số dân tỉnh đó sau 2 năm là: \(\begin{array}{l}800 + 800r\% + (800 + 800r\% ).r\% \\ = 800 + 1600.r\% + 800.{(r\% )^2} = 800.(1 + 2r\% + {(r\% )^2})\\ = 800{(r\% + 1)^2}\end{array}\)
- Số dân tỉnh đó sau 5 năm là: \(800.{(1 + r?\% )^5}\)
b) Ước tính số dân của tỉnh đó sau 5 năm nữa với \(r\% = 1,5\% \)là:
\(800.{(1 + 0,015)^5} = 800.(1 + {5.1^4}.0,015) = 860\) (nghìn người)

Từ dãy số liệu ta có bảng phân bố tần số-tần suất ghép lớp sau đây:
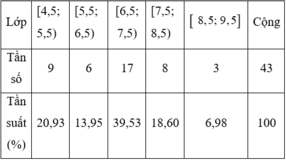
Nhìn vào bảng ta thấy hình chữ nhật đáy [6,5; 7,5) có tần số 17 là lớn nhất. Đáp án là C.

a) Gọi hàm số bậc hai cần tìm là: \(y = a{t^2} + bt + c.\)
Ta có: đỉnh \(I\left( {0;3,2} \right)\) và đi qua điểm \(\left( {1;4} \right)\)
nên \(\left\{ {\begin{array}{*{20}{c}}{ - \frac{b}{{2a}} = 0}\\{c = 3,2}\\{a + b + c = 4}\end{array}} \right.\,\, \Leftrightarrow \,\,\left\{ {\begin{array}{*{20}{c}}{b = 0}\\{c = 3,2}\\{a + c = 4}\end{array}\,\,} \right. \Leftrightarrow \,\,\left\{ {\begin{array}{*{20}{c}}{a = 0,8}\\{b = 0}\\{c = 3,2}\end{array}} \right.\)
Vậy hàm số cần tìm là: \(y = 0,8{t^2} + 3,2\)
b) Thời gian từ năm 2018 đến năm 2024 là: \(t = 2024 - 2018 = 6\) năm
Số lượng máy tính xách tay bán được trong năm 2024 là:
\(0,{8.6^2} + 3,2 = 32\) nghìn chiếc
c) Năm bán đượng vượt mức 52 nghìn chiếc máy tính là:
\(\begin{array}{l}0,8{t^2} + 3,2 > 52\\ \Leftrightarrow \,\,0,8{t^2} - 48,8 > 0\\ \Leftrightarrow \,\,t \in \left( { - \infty ; - \sqrt {61} } \right) \cup \left( {\sqrt {61} ; + \infty } \right)\end{array}\)
Vì \(t > 0\) nên \(t \in \left( {\sqrt {61} ; + \infty } \right)\) hay \(t > \sqrt {61} \approx 7,8\).
Từ năm thứ 8 hay năm 2026 thì số lượng máy tính xách tay bán ra vượt mức 52 nghìn chiếc.

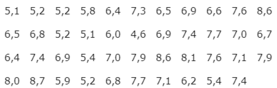
a.Số trung bình của dãy số liệu trên là:
(0,81 + 0,97 + 1,09 +1,19 +1,25 + 1,27 +1,79+1,81+1,85+2,01+7,52):11 = 1,96
b) Trong các số liệu có một giá trị bất thường so với các giá trị còn lại là 7,52 do đó ảnh hưởng đến giá trị trung bình của số liệu. Dẫn đến có sự chênh lệch giữa giá trị trung bình và trung vị.
c) Trung bình và trung vị là các thuật ngữ thống kê có vai trò hơi giống nhau trong việc hiểu xu hướng trung tâm của một tập hợp thống kê. Nhưng có giá trị 7,52 là giá trị khác biệt so với các giá trị còn lại nên gây ảnh hưởng đến số trung bình. Do đó ta nên sử dụng số trung vị để đại diện cho dân số các tỉnh thuộc Đồng bằng Bắc Bộ.
a.Số trung bình của dãy số liệu trên là:
(0,81 + 0,97 + 1,09 +1,19 +1,25 + 1,27 +1,79+1,81+1,85+2,01+7,52):11 = 1,96
b) Trong các số liệu có một giá trị bất thường so với các giá trị còn lại là 7,52 do đó ảnh hưởng đến giá trị trung bình của số liệu. Dẫn đến có sự chênh lệch giữa giá trị trung bình và trung vị.
c) Trung bình và trung vị là các thuật ngữ thống kê có vai trò hơi giống nhau trong việc hiểu xu hướng trung tâm của một tập hợp thống kê. Nhưng có giá trị 7,52 là giá trị khác biệt so với các giá trị còn lại nên gây ảnh hưởng đến số trung bình. Do đó ta nên sử dụng số trung vị để đại diện cho dân số các tỉnh thuộc Đồng bằng Bắc bộ
Trên mạng có nhaa thầy
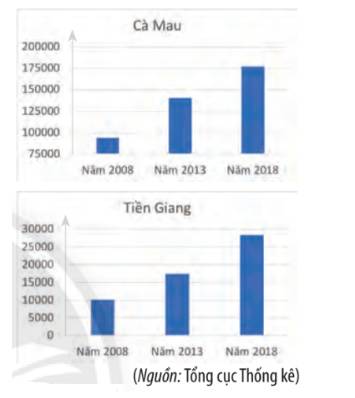

a)
Phát biểu i sai vì ở Tiền Giang sản lượng các năm đều nhỏ hơn 30 000 tấn, còn ở Cà Mau sản lượng các năm đều lớn hơn 75 000 tấn.
Phát biểu ii sai do sản lượng nuôi tôm ở Cà Mau năm 2018 là 175 000 tấn gấp gần 2 lần năm 2008 là 95 000 tấn.
Phát biểu iii đúng do sản lượng nuôi tôm ở Tiền Giang năm 2018 là 28 500 tấn gấp hơn 2,5 lần năm 2008 là 10 000 tấn.
Phát biểu iv đúng do sản lượng nuôi tôm ở Tiền Giang năm 2008 là 10000 tấn, năm 2013 là 17 500 tấn và năm 2018 là 28 500 tấn, đều tăng trên 50% so với năm cũ.
Phát biểu v sai do từ năm 2013 đến 2018, tỉnh Cà Mau tăng 175 000 – 140 000 = 35 000 tấn, tương ứng 25% còn tỉnh Tiền Giang, tăng (28 500 – 17 500) : 17 500 = 63%
b)
Để so sánh sản lượng nuôi tôm của hai tỉnh Cà Mau và Tiền Giang, ta nên sử dụng loại biểu đồ cột kép.